Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Etudes de fonctions - Exercice 3

13 min
25
Soit ff la fonction définie sur R∗\mathbb{R^{*}} par : f(x)=x+2+81xf\left(x\right)=x+2+\frac{81}{x}
Question 1

Montrer que pour tout réel xx non nul, on a : f′(x)=(x−9)(x+9)x2f'\left(x\right)=\frac{\left(x-9\right)\left(x+9\right)}{x^{2} }

Correction
  • (nombrex)′=−nombrex2\left(\frac{\red{\text{nombre}}}{x} \right)^{'} =-\frac{{\red{\text{nombre}}}}{x^{2} }
    • Nous avons f(x)=x+2+81xf\left(x\right)=x+2+\frac{\red{81}}{x} alors :
    f′(x)=1−81x2f'\left(x\right)=1-\frac{\red{81}}{x^{2} }
    . Nous allons tout mettre au même dénominateur .
    f′(x)=11−81x2f'\left(x\right)=\frac{1}{1} -\frac{81}{x^{2} }
    f′(x)=1×x2x2−81x2f'\left(x\right)=\frac{1\times x^{2} }{x^{2} } -\frac{81}{x^{2} }
    f′(x)=x2−81x2f'\left(x\right)=\frac{x^{2} -81}{x^{2} }
    f′(x)=x2−92x2f'\left(x\right)=\frac{{\color{blue}x}^{2} -{\color{red}9}^{2} }{x^{2} } . Ici on fait apparaître une identité remarquable afin de factoriser le numérateur.
    • a2−b2=(a−b)(a+b){\color{blue}a}^{2} -{\color{red}b}^{2}=\left({\color{blue}a}-{\color{red}b}\right)\left({\color{blue}a}+{\color{red}b}\right)
    Ainsi :
    f′(x)=(x−9)(x+9)x2f'\left(x\right)=\frac{\left({\color{blue}x}-{\color{red}9}\right)\left({\color{blue}x}+{\color{red}9}\right)}{x^{2} }
    Question 2

    Expliquer pourquoi, pour tout réel xx non nul, f′(x)f'\left(x\right) a le même signe que (x−9)(x+9)\left(x-9\right)\left(x+9\right) .

    Correction
    Le dénominateur x2x^{2} s'annule pour x=0x=0 qui est la valeur interdite . C'est pour cette raison que nous travaillons sur R∗\mathbb{R^{*}} .
    Le signe de x2x^{2} est alors strictement positif\red{\text{strictement positif}}.
    Donc le signe de f(x)f\left(x\right) ne deˊpend alors que de son numeˊrateur\red{\text{ne dépend alors que de son numérateur}} (x−9)(x+9)\left(x-9\right)\left(x+9\right) .
    Dans le tableau il y aura une double barre pour la valeur 00 .
    Question 3

    Etudier le signe de f′f' pour tout réel xx non nul.

    Correction
  • Premieˋrement :\red{\text{Premièrement :}}
    • x−9=0⇔x=9x-9=0\Leftrightarrow x=9
    Soit x↦x−9x\mapsto x-9 est une fonction affine croissante car son coefficient directeur a=1>0a=1>0. (Cela signifie que la fonction MONTE donc on commencera dans la ligne x−9x-9 par le signe (−)\left(-\right) et dès que l'on dépasse la valeur x=9x=9 on mettra le signe (+)\left(+\right) dans le tableau de signe.)
  • Deuxieˋmement :\red{\text{Deuxièmement :}}
    • x+9=0⇔x=−9x+9=0\Leftrightarrow x=-9
    Soit x↦x+9x\mapsto x+9 est une fonction affine croissante car son coefficient directeur a=1>0a=1>0. (Cela signifie que la fonction MONTE donc on commencera dans la ligne x+9x+9 par le signe (−)\left(-\right) et dès que l'on dépasse la valeur x=−9x=-9 on mettra le signe (+)\left(+\right) dans le tableau de signe.)
    Le tableau du signe de f′(x)f'\left(x\right) est alors :
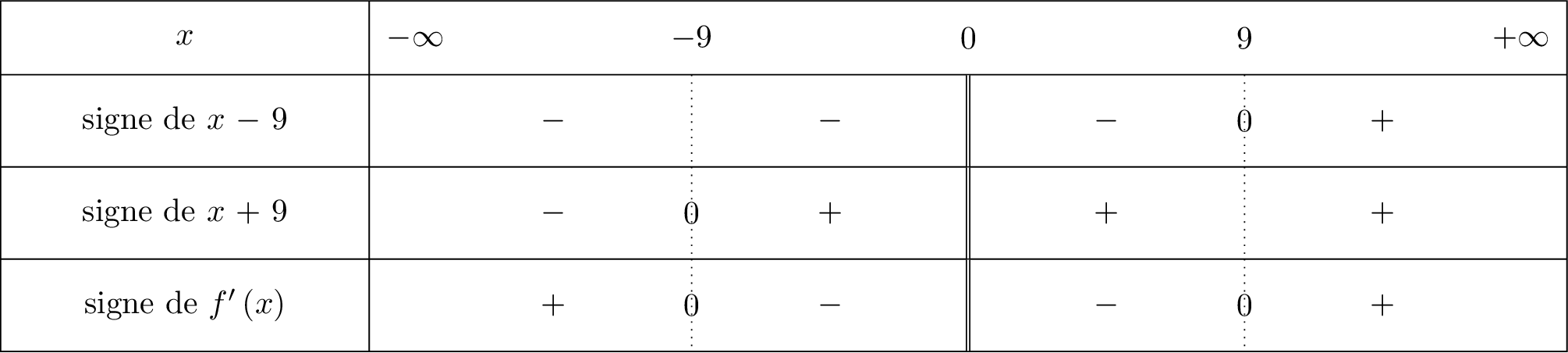
    Question 4

    Pour tout réel xx non nul, en déduire le sens de variation de ff.

    Correction
    • Si f′f' est négative sur [a;b]\left[a;b\right] alors ff est décroissante sur [a;b]\left[a;b\right].
    • Si f′f' est positive sur [a;b]\left[a;b\right] alors ff est croissante sur [a;b]\left[a;b\right].

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.