Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Déterminer la forme exponentielle d'un nombre complexe - Exercice 1

15 min
30
Déterminer la forme exponentielle des nombres complexes suivants :
Question 1

z1=3+iz_{1} =\sqrt{3} +i

Correction
Premieˋre eˊtape :\red{\text{Première étape :}} Calcul du module de z1z_{1}
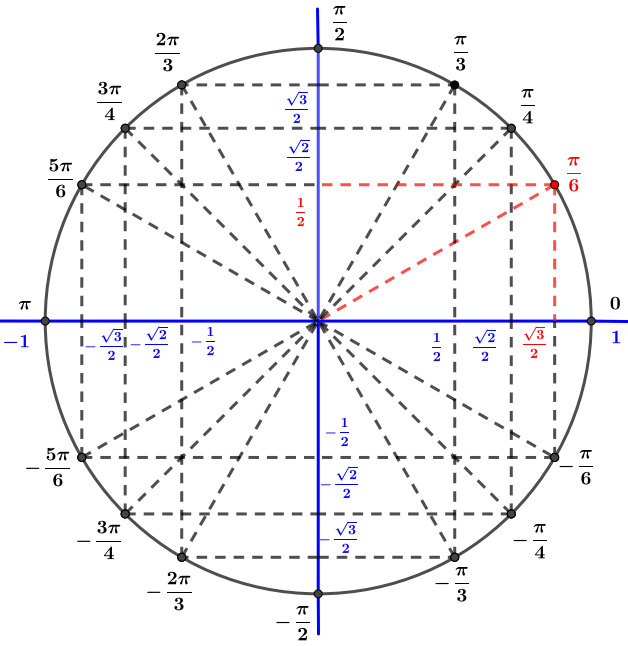
    zz est un nombre complexe sous forme algébrique x+iyx+iy où xx et yy sont des réels.
  • On appelle module\red{\text{module}} de zz le nombre réel positif ∣z∣=x2+y2\left|z\right|=\sqrt{x^{2} +y^{2} } .
    • ∣z1∣=(3)2+12=2\left|z_{1} \right|=\sqrt{\left(\sqrt{3} \right)^{2} +1^{2} } =2
    Deuxieˋme eˊtape :\red{\text{Deuxième étape :}} Calcul d'un argument de z1z_{1}
    Pour l'argument θ\theta on sait que {cos⁡(θ)=partie reˊelle de z1module de z1sin⁡(θ)=partie imaginaire de z1module de z1\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {\frac{\text{partie réelle de } z_{1}}{\text{module de } z_{1}} } \\ {\sin \left(\theta \right)} & {=} & {\frac{\text{partie imaginaire de } z_{1}}{\text{module de } z_{1} } } \end{array}\right.
    On a donc {cos⁡(θ)=32sin⁡(θ)=12\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {\frac{\sqrt{3} }{2} } \\ {\sin \left(\theta \right)} & {=} & {\frac{1}{2} } \end{array}\right.
    Avec le cercle trigonométrique on en déduit que
    θ=π6[2π]\theta =\frac{\pi }{6} \left[2\pi \right]
    [2π]\left[2\pi \right] signifie modulo 2π2\pi
    Soit zz un nombre complexe dont le module est ∣z∣\left|z\right| et θ\theta un argument de zz.
    • L'écriture exponentielle de zz est alors z=∣z∣eiθz=\left|z\right|e^{i\theta }
    Il en résulte donc que l'écriture exponentielle de z1z_{1} est alors :
    z1=2eiπ6z_{1}=2e^{i\frac{\pi }{6} }
    Question 2

    z2=2+2iz_{2} =2 +2i

    Correction
    Premieˋre eˊtape :\red{\text{Première étape :}} Calcul du module de z2z_{2}
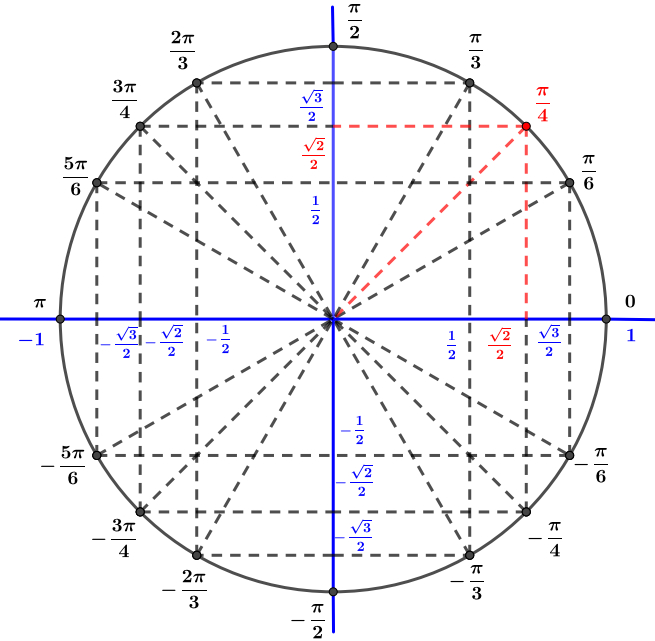
      zz est un nombre complexe sous forme algébrique x+iyx+iy où xx et yy sont des réels.
  • On appelle module\red{\text{module}} de zz le nombre réel positif ∣z∣=x2+y2\left|z\right|=\sqrt{x^{2} +y^{2} } .
    • ∣z2∣=22+22=8\left|z_{2} \right|=\sqrt{2^{2} +2^{2} } =\sqrt{8} ainsi ∣z2∣=22\left|z_{2} \right|=2\sqrt{2}
    Deuxieˋme eˊtape :\red{\text{Deuxième étape :}} Calcul d'un argument de z2z_{2}
    Pour l'argument θ\theta on sait que {cos⁡(θ)=partie reˊelle de z2module de z2sin⁡(θ)=partie imaginaire de z2module de z2\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {\frac{\text{partie réelle de } z_{2}}{\text{module de } z_{2}} } \\ {\sin \left(\theta \right)} & {=} & {\frac{\text{partie imaginaire de } z_{2}}{\text{module de } z_{2} } } \end{array}\right.
    On a donc :
    {cos⁡(θ)=222sin⁡(θ)=222\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {\frac{2 }{2\sqrt{2} } } \\ {\sin \left(\theta \right)} & {=} & {\frac{2}{2\sqrt{2} } } \end{array}\right.
    {cos⁡(θ)=22sin⁡(θ)=22\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {\frac{\sqrt{2} }{2 } } \\ {\sin \left(\theta \right)} & {=} & {\frac{\sqrt{2}}{2}}\end{array}\right.
    Avec le cercle trigonométrique on en déduit que
    θ=π4[2π]\theta =\frac{\pi }{4} \left[2\pi \right]
    [2π]\left[2\pi \right] signifie modulo 2π2\pi
    Soit zz un nombre complexe dont le module est ∣z∣\left|z\right| et θ\theta un argument de zz.
    • L'écriture exponentielle de zz est alors z=∣z∣eiθz=\left|z\right|e^{i\theta }
    Il en résulte donc que l'écriture exponentielle de z2z_{2} est alors :
    z2=22eiπ4z_{2}=2\sqrt{2}e^{i\frac{\pi }{4} }
    Question 3

    z3=3−3i3z_{3} =3-3i\sqrt{3}

    Correction
    Premieˋre eˊtape :\red{\text{Première étape :}} Calcul du module de z3z_{3}
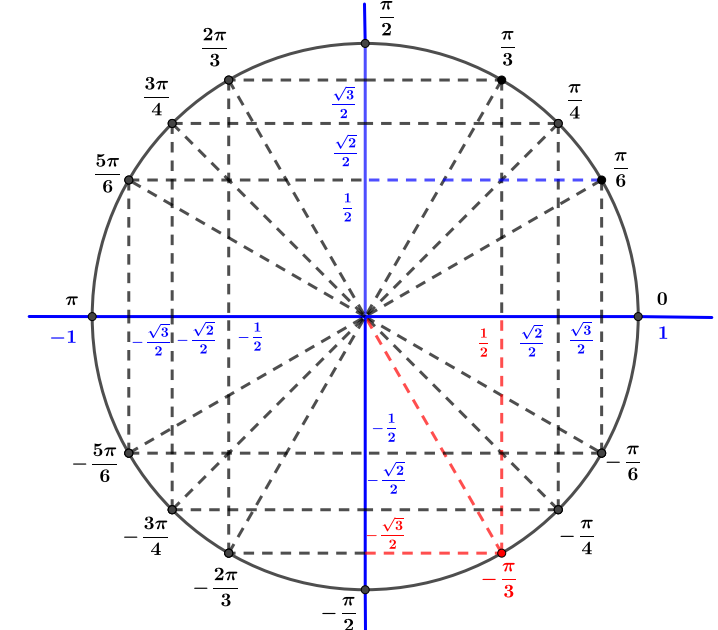
      zz est un nombre complexe sous forme algébrique x+iyx+iy où xx et yy sont des réels.
  • On appelle module\red{\text{module}} de zz le nombre réel positif ∣z∣=x2+y2\left|z\right|=\sqrt{x^{2} +y^{2} } .
    • ∣z3∣=32+(−33)2=36\left|z_{3} \right|=\sqrt{3^{2} +\left(-3\sqrt{3} \right)^{2} } =\sqrt{36} ainsi ∣z3∣=6\left|z_{3} \right|=6
    Deuxieˋme eˊtape :\red{\text{Deuxième étape :}} Calcul d'un argument de z3z_{3}
    Pour l'argument θ\theta on sait que {cos⁡(θ)=partie reˊelle de z3module de z3sin⁡(θ)=partie imaginaire de z3module de z3\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {\frac{\text{partie réelle de } z_{3}}{\text{module de } z_{3}} } \\ {\sin \left(\theta \right)} & {=} & {\frac{\text{partie imaginaire de } z_{3}}{\text{module de } z_{3} } } \end{array}\right.
    On a donc :
    {cos⁡(θ)=36sin⁡(θ)=−336\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {\frac{3 }{6 } } \\ {\sin \left(\theta \right)} & {=} & {\frac{-3\sqrt{3}}{6 } } \end{array}\right.
    {cos⁡(θ)=12sin⁡(θ)=−32\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {\frac{1 }{2 } } \\ {\sin \left(\theta \right)} & {=} & {-\frac{\sqrt{3}}{2}}\end{array}\right.
    Avec le cercle trigonométrique on en déduit que
    θ=−π3[2π]\theta =-\frac{\pi }{3} \left[2\pi \right]
    [2π]\left[2\pi \right] signifie modulo 2π2\pi
    Soit zz un nombre complexe dont le module est ∣z∣\left|z\right| et θ\theta un argument de zz.
    • L'écriture exponentielle de zz est alors z=∣z∣eiθz=\left|z\right|e^{i\theta }
    Il en résulte donc que l'écriture exponentielle de z3z_{3} est alors :
    z3=6e−iπ3z_{3}=6e^{-i\frac{\pi }{3} }
    Question 4

    z4=−7iz_{4} =-7i

    Correction
    Premieˋre eˊtape :\red{\text{Première étape :}} Calcul du module de z4z_{4}
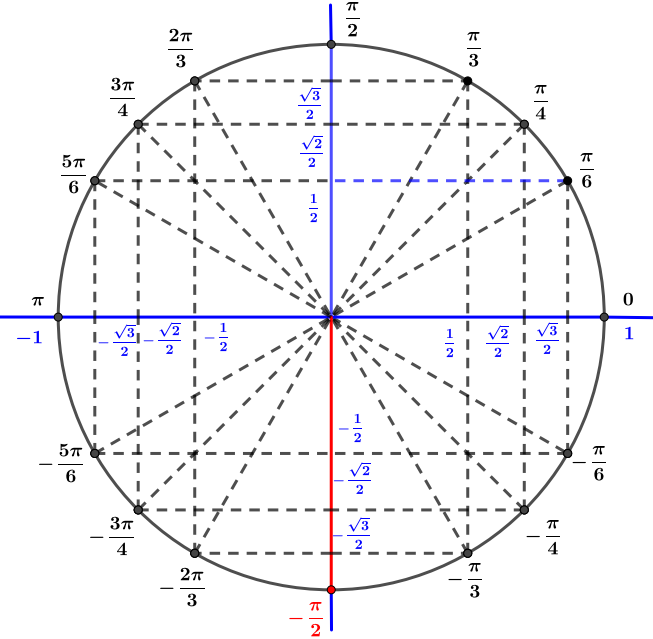
      zz est un nombre complexe sous forme algébrique x+iyx+iy où xx et yy sont des réels.
  • On appelle module\red{\text{module}} de zz le nombre réel positif ∣z∣=x2+y2\left|z\right|=\sqrt{x^{2} +y^{2} } .
    • ∣z4∣=02+(−7)2=49\left|z_{4} \right|=\sqrt{0^{2} +\left(-7 \right)^{2} } =\sqrt{49} ainsi ∣z4∣=7\left|z_{4} \right|=7
    Deuxieˋme eˊtape :\red{\text{Deuxième étape :}} Calcul d'un argument de z4z_{4}
    Pour l'argument θ\theta on sait que {cos⁡(θ)=partie reˊelle de z4module de z4sin⁡(θ)=partie imaginaire de z4module de z4\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {\frac{\text{partie réelle de } z_{4}}{\text{module de } z_{4}} } \\ {\sin \left(\theta \right)} & {=} & {\frac{\text{partie imaginaire de } z_{4}}{\text{module de } z_{4} } } \end{array}\right.
    On a donc :
    {cos⁡(θ)=07sin⁡(θ)=−77\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {\frac{0}{7 } } \\ {\sin \left(\theta \right)} & {=} & {\frac{-7}{7}} \end{array}\right.
    {cos⁡(θ)=0sin⁡(θ)=−1\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {0 } \\ {\sin \left(\theta \right)} & {=} & {-1}\end{array}\right.
    Avec le cercle trigonométrique on en déduit que
    θ=−π2[2π]\theta =-\frac{\pi }{2} \left[2\pi \right]
    [2π]\left[2\pi \right] signifie modulo 2π2\pi
    Soit zz un nombre complexe dont le module est ∣z∣\left|z\right| et θ\theta un argument de zz.
    • L'écriture exponentielle de zz est alors z=∣z∣eiθz=\left|z\right|e^{i\theta }
    Il en résulte donc que l'écriture exponentielle de z4z_{4} est alors :
    z4=7e−iπ2z_{4}=7e^{-i\frac{\pi }{2} }
    Question 5

    z5=−3z_{5} =-3

    Correction
    Premieˋre eˊtape :\red{\text{Première étape :}} Calcul du module de z5z_{5}
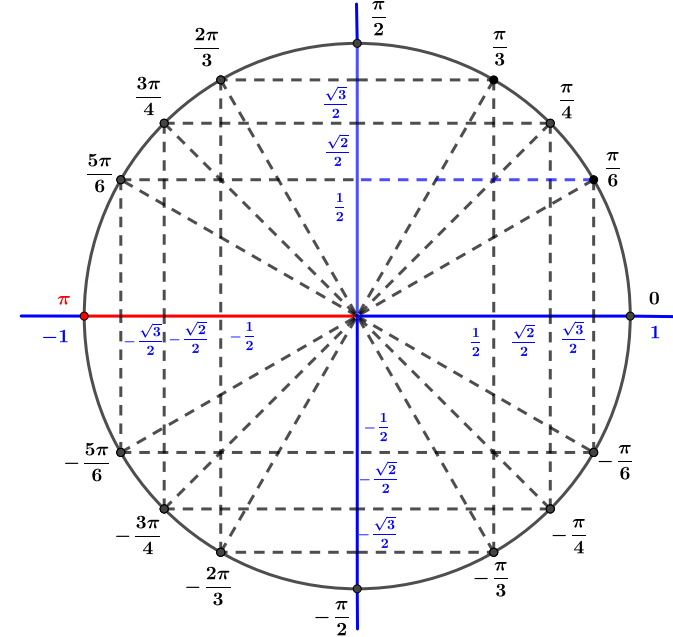
      zz est un nombre complexe sous forme algébrique x+iyx+iy où xx et yy sont des réels.
  • On appelle module\red{\text{module}} de zz le nombre réel positif ∣z∣=x2+y2\left|z\right|=\sqrt{x^{2} +y^{2} } .
    • ∣z5∣=(−3)2+02=9\left|z_{5} \right|=\sqrt{\left(-3 \right)^{2} +0^{2} } =\sqrt{9} ainsi ∣z5∣=3\left|z_{5} \right|=3
    Deuxieˋme eˊtape :\red{\text{Deuxième étape :}} Calcul d'un argument de z5z_{5}
    Pour l'argument θ\theta on sait que {cos⁡(θ)=partie reˊelle de z5module de z5sin⁡(θ)=partie imaginaire de z5module de z5\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {\frac{\text{partie réelle de } z_{5}}{\text{module de } z_{5}} } \\ {\sin \left(\theta \right)} & {=} & {\frac{\text{partie imaginaire de } z_{5}}{\text{module de } z_{5} } } \end{array}\right.
    On a donc :
    {cos⁡(θ)=−33sin⁡(θ)=03\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {\frac{-3}{3 } } \\ {\sin \left(\theta \right)} & {=} & {\frac{0}{3}} \end{array}\right.
    {cos⁡(θ)=−1sin⁡(θ)=0\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {-1 } \\ {\sin \left(\theta \right)} & {=} & {0}\end{array}\right.
    Avec le cercle trigonométrique on en déduit que
    θ=−π[2π]\theta =-\pi\left[2\pi \right]
    [2π]\left[2\pi \right] signifie modulo 2π2\pi
    Soit zz un nombre complexe dont le module est ∣z∣\left|z\right| et θ\theta un argument de zz.
    • L'écriture exponentielle de zz est alors z=∣z∣eiθz=\left|z\right|e^{i\theta }
    Il en résulte donc que l'écriture exponentielle de z5z_{5} est alors :
    z5=3e−iπz_{5}=3e^{-i\pi }
    Question 6

    z6=−1+iz_{6} =-1 +i

    Correction
    Premieˋre eˊtape :\red{\text{Première étape :}} Calcul du module de z6z_{6}
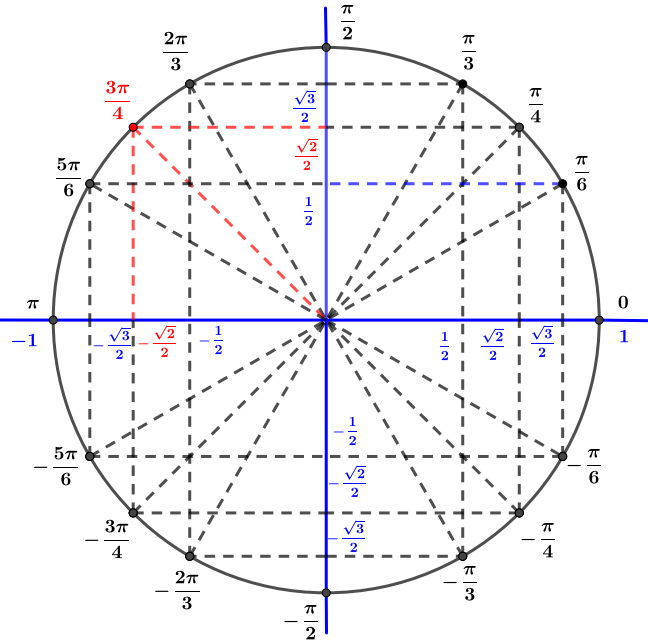
      zz est un nombre complexe sous forme algébrique x+iyx+iy où xx et yy sont des réels.
  • On appelle module\red{\text{module}} de zz le nombre réel positif ∣z∣=x2+y2\left|z\right|=\sqrt{x^{2} +y^{2} } .
    • ∣z6∣=(−1)2+12=2\left|z_{6} \right|=\sqrt{\left(-1\right)^{2} +1^{2} } =\sqrt{2}
    Deuxieˋme eˊtape :\red{\text{Deuxième étape :}} Calcul d'un argument de z6z_{6}
    Pour l'argument θ\theta on sait que {cos⁡(θ)=partie reˊelle de z6module de z6sin⁡(θ)=partie imaginaire de z6module de z6\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {\frac{\text{partie réelle de } z_{6}}{\text{module de } z_{6}} } \\ {\sin \left(\theta \right)} & {=} & {\frac{\text{partie imaginaire de } z_{6}}{\text{module de } z_{6} } } \end{array}\right.
    On a donc :
    {cos⁡(θ)=−12sin⁡(θ)=12\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {\frac{-1}{\sqrt{2} } } \\ {\sin \left(\theta \right)} & {=} & {\frac{1}{\sqrt{2} } } \end{array}\right.
    {cos⁡(θ)=−22sin⁡(θ)=22\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {-\frac{\sqrt{2} }{2 } } \\ {\sin \left(\theta \right)} & {=} & {\frac{\sqrt{2}}{2}}\end{array}\right.
    Avec le cercle trigonométrique on en déduit que
    θ=3π4[2π]\theta =\frac{3\pi }{4} \left[2\pi \right]
    [2π]\left[2\pi \right] signifie modulo 2π2\pi
    Soit zz un nombre complexe dont le module est ∣z∣\left|z\right| et θ\theta un argument de zz.
    • L'écriture exponentielle de zz est alors z=∣z∣eiθz=\left|z\right|e^{i\theta }
    Il en résulte donc que l'écriture exponentielle de z6z_{6} est alors :
    z6=2ei3π4z_{6}=\sqrt{2}e^{i\frac{3\pi }{4} }