Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Baccalauréat STI2D Métropole Juin 2021 - Exercice 1
10 min
25
Le plan complexe est muni d’un repère orthonormé direct . On considère les points et d’affixes respectives : et .
Question 1
Les points , et sont-ils alignés ?
Correction
Dans un premier temps, nous allons donner la forme algébrique de .
Ainsi :
Si les points , et sont alignés alors les vecteurs et doivent être colinéaires.
Autrement dit, il existe un réel vérifiant la relation vectorielle .
Nous avons : ; et car est l'origine du repère.
D'une part :
Ainsi :
D'autre part :
Ainsi :
Nous allons transformer l'expression de .
Soit :
On remarque que :
. Nous allons maintenant factoriser par .
. Nous allons factoriser par . Ce qui nous donne.
Enfin :
Il en résulte donc que les vecteurs et sont bien colinéaires.
Finalement, les points , et sont alignés .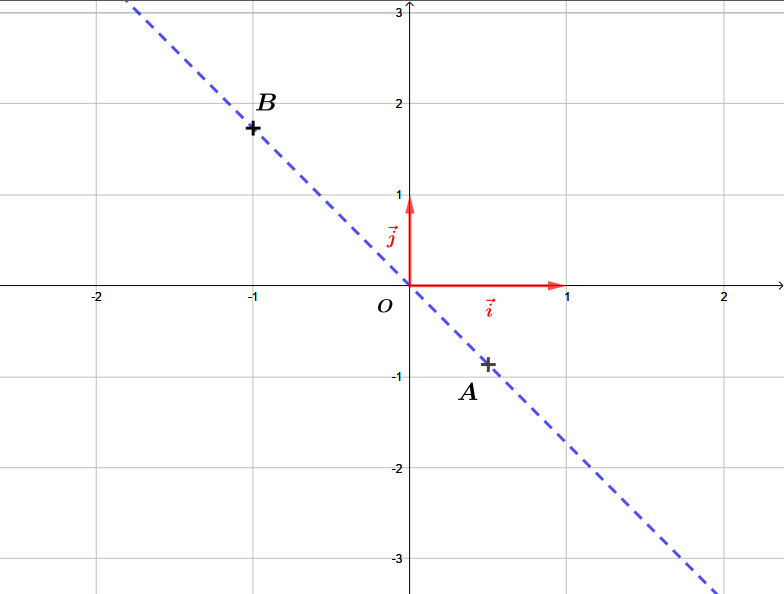
Ainsi :
Si les points , et sont alignés alors les vecteurs et doivent être colinéaires.
Autrement dit, il existe un réel vérifiant la relation vectorielle .
- Si et sont les affixes respectives des points et dans un repère orthonormé direct , alors l'affixe du vecteur est égale à .
D'une part :
Ainsi :
D'autre part :
Ainsi :
Nous allons transformer l'expression de .
Soit :
On remarque que :
. Nous allons maintenant factoriser par .
. Nous allons factoriser par . Ce qui nous donne.
Enfin :
Il en résulte donc que les vecteurs et sont bien colinéaires.
Finalement, les points , et sont alignés .
