Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Baccalauréat STI2D Centres étrangers 13 mars 2023 - Exercice 1
20 min
40
On considère les nombres complexes et , où désigne le nombre complexe de module et d’argument .
Question 1
Écrire sous forme exponentielle .
Correction
Calcul du module de
On appelle de le nombre réel positif .
Calcul d'un argument de
Pour l'argument on sait que
On a donc
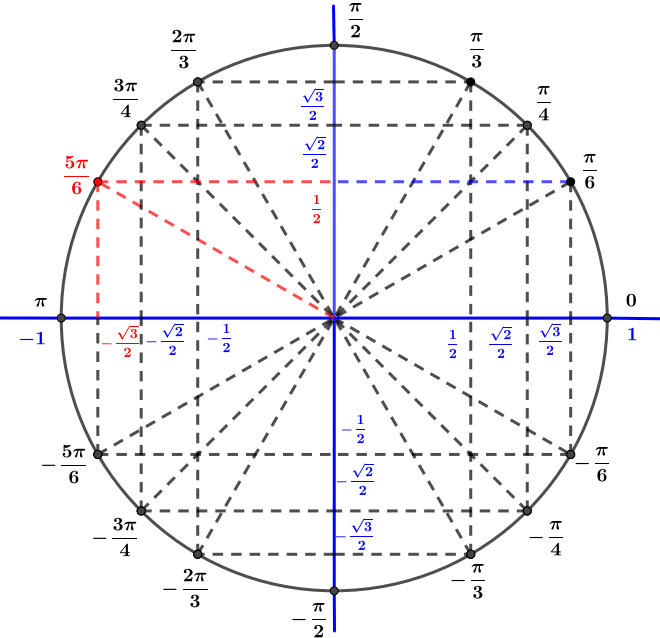
Avec le cercle trigonométrique on en déduit que
- est un nombre complexe sous forme algébrique où et sont des réels.
Calcul d'un argument de
Pour l'argument on sait que
On a donc
Avec le cercle trigonométrique on en déduit que
signifie modulo

Soit un nombre complexe dont le module est et un argument de .
Il en résulte donc que l'écriture exponentielle de est alors : - L'écriture exponentielle de est alors
Question 2
En déduire une écriture du nombre complexe .
Correction
équivaut successivement à :
Or
Ainsi :
Soient , , et quatre réels avec , on a alors :
Or
Ainsi :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.