Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
- Tous les niveaux>
- Enseignement de spécialité>
- Les fonctions circulaires ou les fonctions trigonométriques
Comment étudier la périodicité d'une fonction - Exercice 2
5 min
15
Question 1
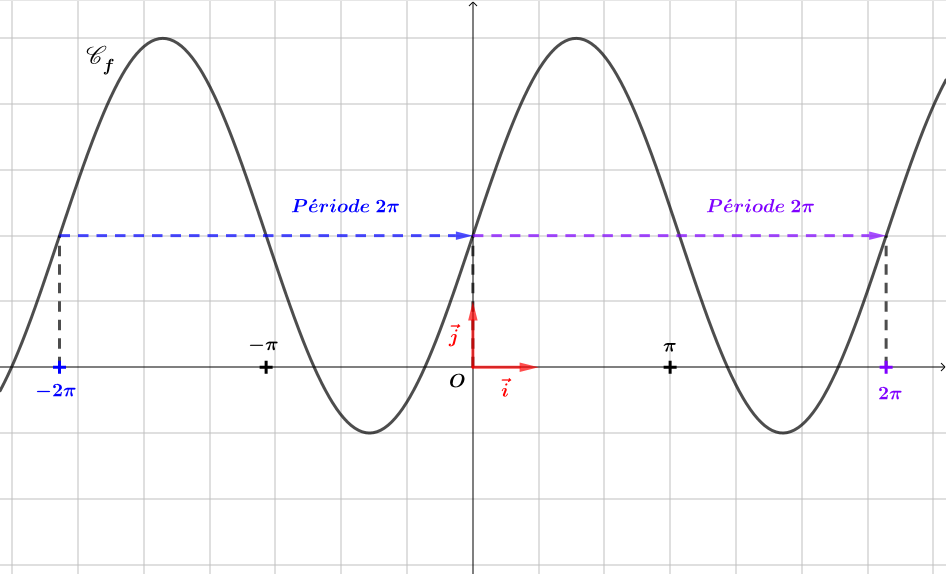
Soit . Montrer que est périodique.
Correction
Il en résulte que
donc est périodique.
Question 2
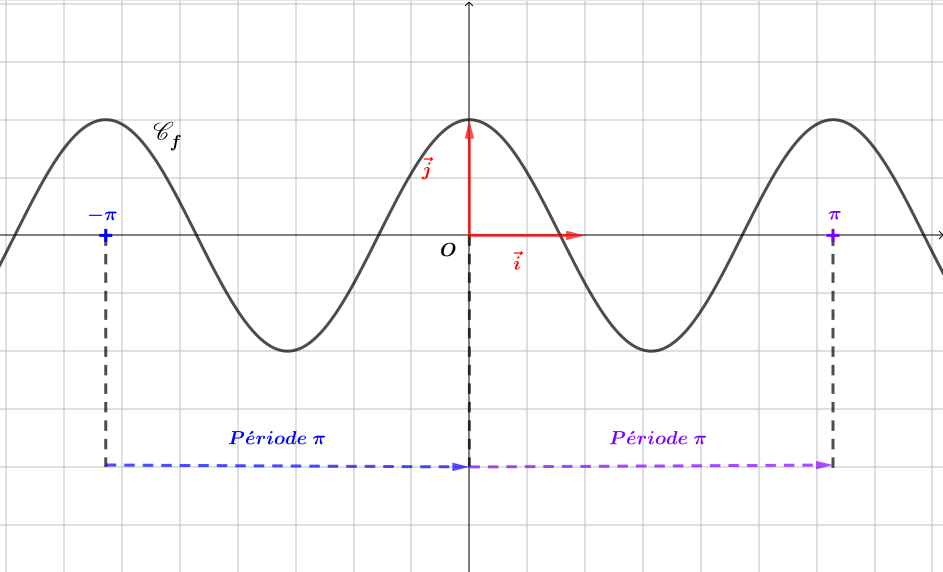
Soit une fontion définie sur par . Montrer que est périodique.
Correction
Il en résulte que
donc est périodique.