Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Exercices types : 11ère partie - Exercice 2

20 min
40
Un responsable étudie l’évolution de la concentration de benzène à la surface du bassin sans intervention extérieure. Il estime que cette concentration diminue de manière naturelle de 7%7\% par jour, notamment par évaporation. La concentration observée le 1010 juin 20202020 est de 6868 microgrammes par litre.
Pour tout entier naturel nn, on note unu_{n} la concentration de benzène, en microgrammes par litre, à la surface du bassin nn jours après le 1010 juin 20202020.
Question 1

Montrer que la suite (un)\left(u_{n}\right) est une suite géométrique dont on précisera le premier terme et la raison.

Correction
La concentration diminue de manière naturelle de 7%7\% par jour. On multiplie donc chaque jour la concentration par le coefficient multiplicateur q=1−17100=0,93q=1-\frac{17}{100}=0,93 .
Chaque terme se déduit du précédent en le multipliant par 0,930,93.
Il en résulte donc que la suite (un)\left(u_{n}\right) est geˊomeˊtrique{\color{blue}\text{géométrique}} de raison q=0,93q=0,93 .
Le 1010 juin 20202020 la concentration est de 6868 µg/L donc le premier terme de la suite est u0=68u_{0}=68.
Question 2

Exprimer un+1u_{n+1} en fonction de unu_{n}.

Correction
Soit (un)\left(u_{n} \right) une suite géométrique.
  • L'expression de un+1u_{n+1} en fonction de unu_{n} est donnée par la relation de récurrence : un+1=un×qu_{n+1} =u_{n}\times q où qq est la raison{\color{blue}\text{raison}} de la suite géométrique.
    • Ainsi :
    un+1=un×0,93u_{n+1} =u_{n}\times0,93
    Finalement :
    un+1=0,93unu_{n+1} =0,93u_{n}

    Question 3

    Déterminer une expression de unu_{n} en fonction de nn.

    Correction
    D'après la question précédente, nous avons montré que la suite (un)\left(u_{n}\right) est une suite géométrique de raison q=0,93q=0,93 et de premier terme u0=68u_{0}=68.
    • L'expression de unu_{n} en fonction de nn est donnée par la formule
      un=u0×qnu_{n} =u_{0} \times q^{n}
    Ainsi :
    un=68×0,93nu_{n} =68\times 0,93^{n}

    Question 4

    Déterminer la concentration de benzène le 1515 juin 20202020 .

    Correction
    Le 1515 juin 20202020 correspond à n=5n=5.
    Ainsi : u5=68×0,935u_{5} =68\times 0,93^{5} d'où :
    u5≈47,3u_{5} \approx47,3

    Question 5
    On propose ci-dessous la partie traitement de deux algorithmes.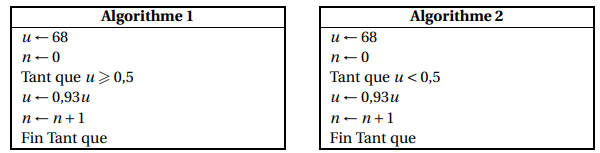

    Quel est celui qui permettrait de déterminer le nombre de jours de fermeture avant que la qualité de l’eau soit devenue excellente? L'eau devient excellente si la concentration est strictement inférieur à 0,50,5.

    Correction
    Dans l’algorithme 22 la condition pour entrer dans la boucle est «u<0,5u <0,5»; or la variable uu est initialisée à 6868 donc on n’entre jamais dans la boucle car 68<0,568<0,5 est une proposition fausse . L’algorithme 22 affichera la valeur 00 pour nn. C’est donc l’algorithme 11 qui permet de déterminer le nombre de jours de fermeture avant que la qualité de l’eau soit devenue excellente.