Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Calculer des coefficients binomiaux à l'aide du triangle de Pascal - Exercice 2
5 min
20
Question 1
Construire le triangle de Pascal jusqu'à .
Correction
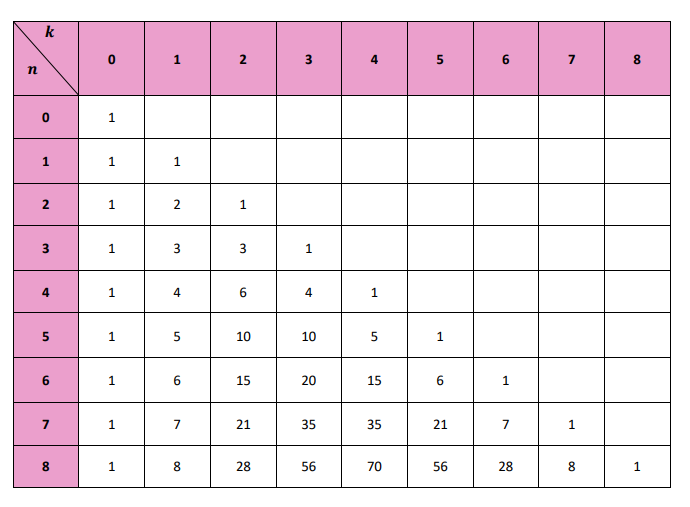
Question 2
Calculer à l'aide du triangle de Pascal :
Correction
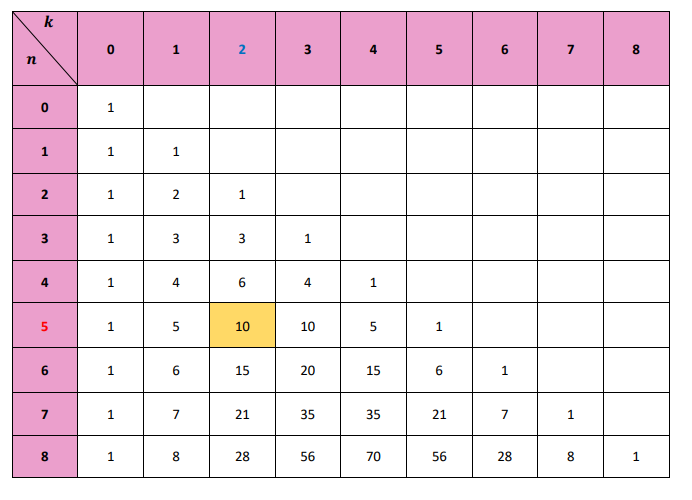
D'après le triangle de pascal, nous pouvons lire que :
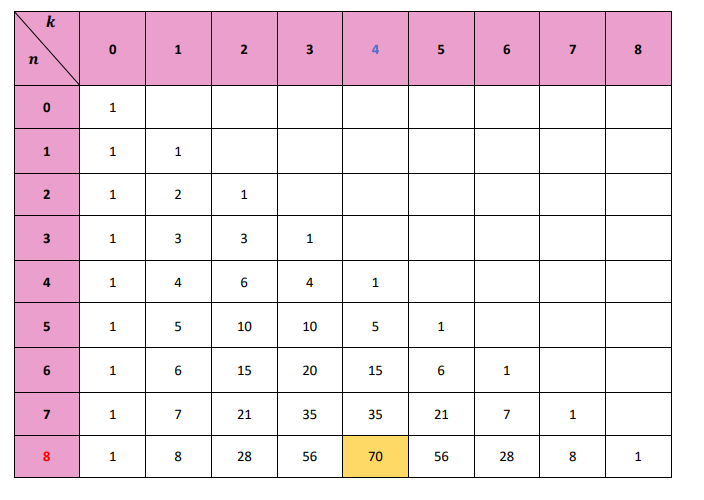
Question 3
Correction
D'après le triangle de pascal, nous pouvons lire que :
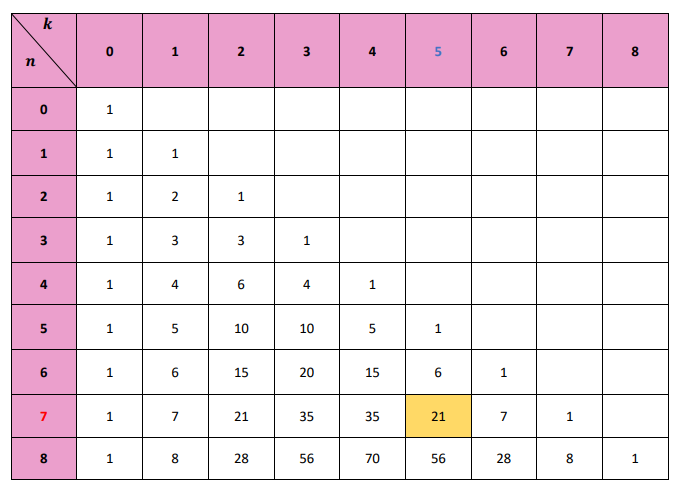
Question 4
Correction
D'après le triangle de pascal, nous pouvons lire que :
Question 5
Correction
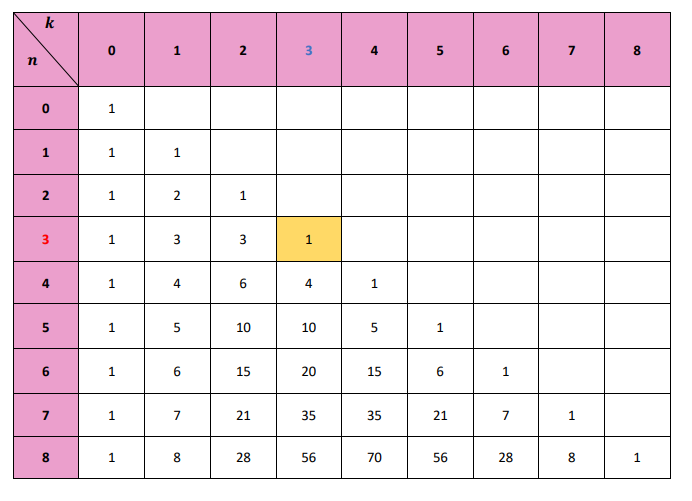
D'après le triangle de pascal, nous pouvons lire que :
Question 6
Correction
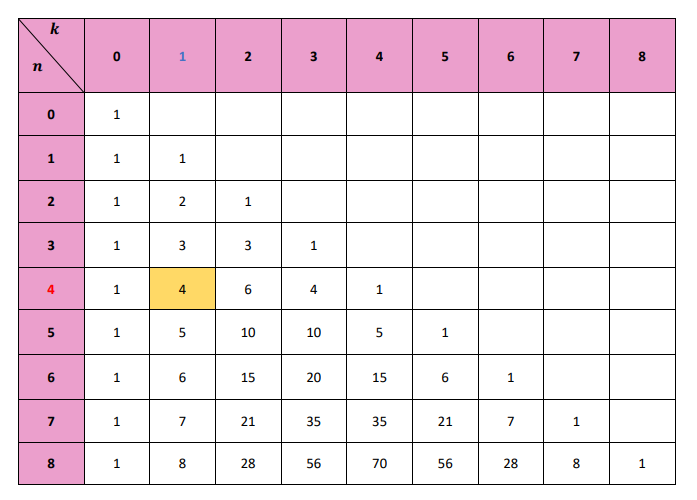
D'après le triangle de pascal, nous pouvons lire que :
Question 7
Correction
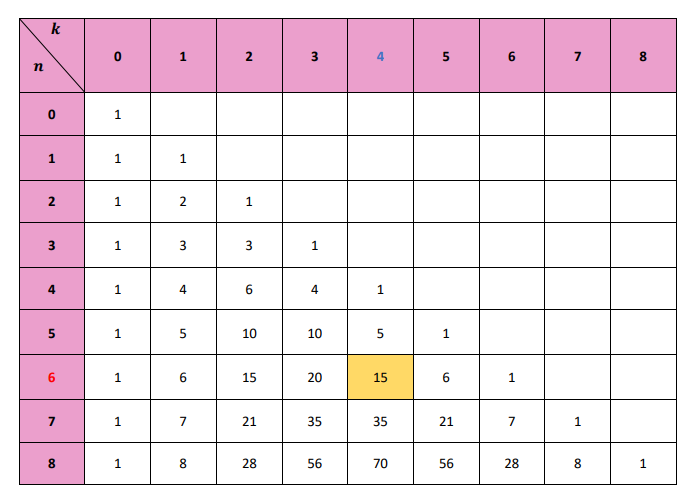
D'après le triangle de pascal, nous pouvons lire que :
Question 8
Correction
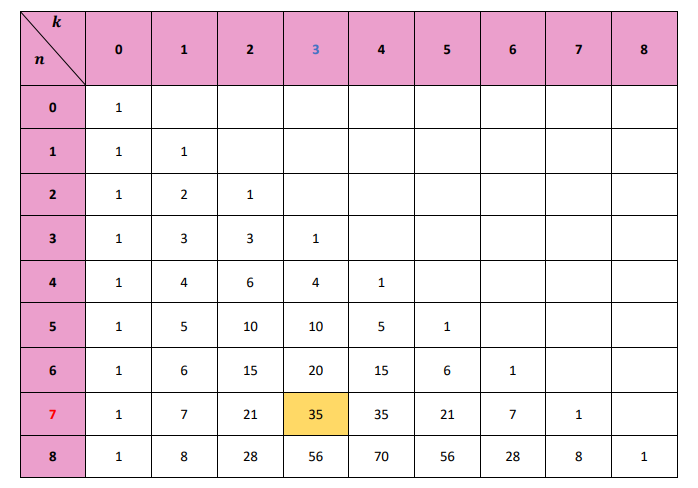
D'après le triangle de pascal, nous pouvons lire que :