Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Fonction paire / fonction impaire - Exercice 1
15 min
20
Etudiez la parité des fonctions suivantes.
Question 1
Correction
est une fonction paire si pour tout réel , on a .
La fonction cosinus est paire.
est une fonction impaire si pour tout réel , on a .
La fonction sinus est impaire.
Attention, une fonction non paire n'est pas obligatoirement impaire et une fonction non impaire n'est pas obligatoirement paire.
Une fonction peut être ni paire, ni impaire.
La fonction est une fonction paire.
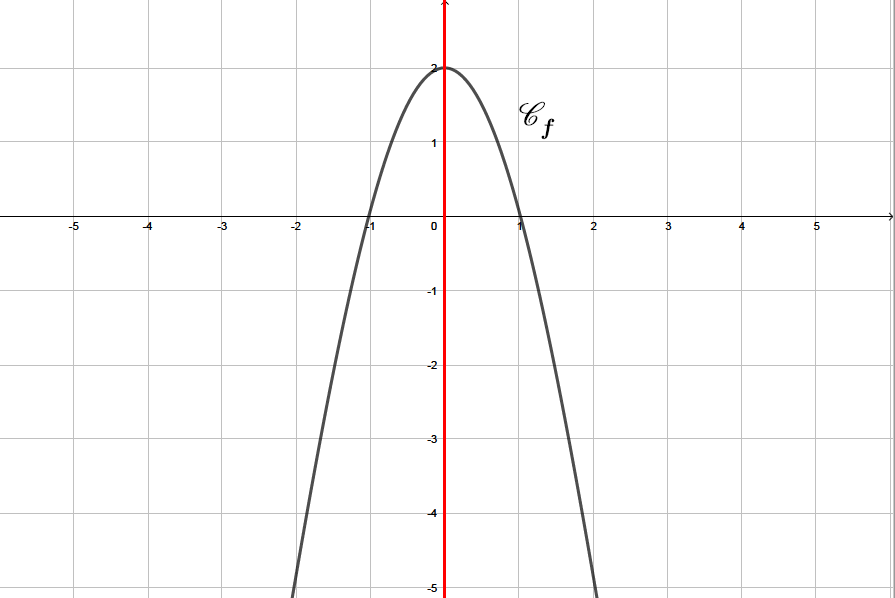
Question 2
Correction
est une fonction paire si pour tout réel , on a .
La fonction cosinus est paire.
est une fonction impaire si pour tout réel , on a .
La fonction sinus est impaire.
Attention, une fonction non paire n'est pas obligatoirement impaire et une fonction non impaire n'est pas obligatoirement paire.
Une fonction peut être ni paire, ni impaire.
La fonction est une fonction impaire.
Question 3
Correction
est une fonction paire si pour tout réel , on a .
La fonction cosinus est paire.
est une fonction impaire si pour tout réel , on a .
La fonction sinus est impaire.
Attention, une fonction non paire n'est pas obligatoirement impaire et une fonction non impaire n'est pas obligatoirement paire.
Une fonction peut être ni paire, ni impaire.
Ainsi :
Enfin :
La fonction est une fonction paire.
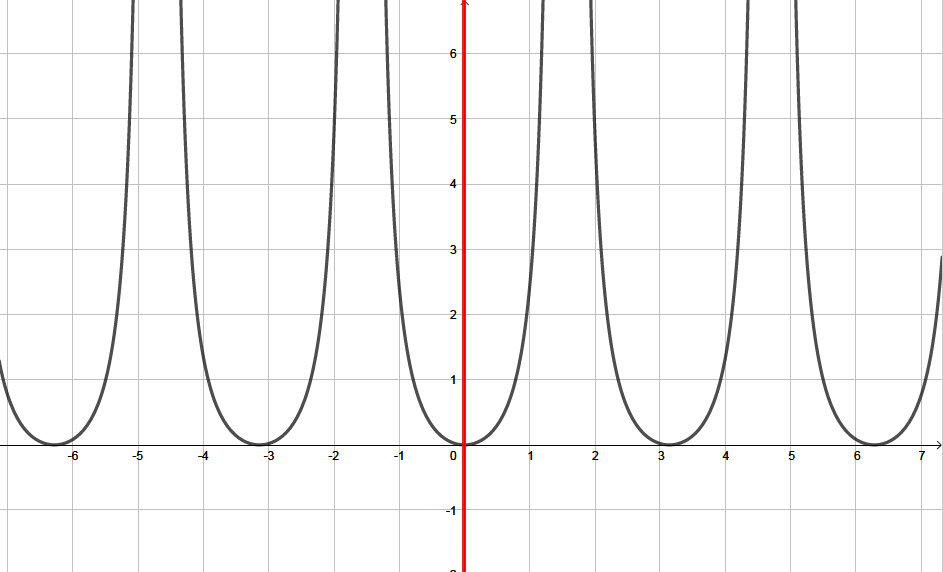
Question 4
Correction
est une fonction paire si pour tout réel , on a .
La fonction cosinus est paire.
est une fonction impaire si pour tout réel , on a .
La fonction sinus est impaire.
Attention, une fonction non paire n'est pas obligatoirement impaire et une fonction non impaire n'est pas obligatoirement paire.
Une fonction peut être ni paire, ni impaire.
Ainsi :
équivaut successivement à :
car
Ici
et
La fonction n'est ni paire ni impaire.
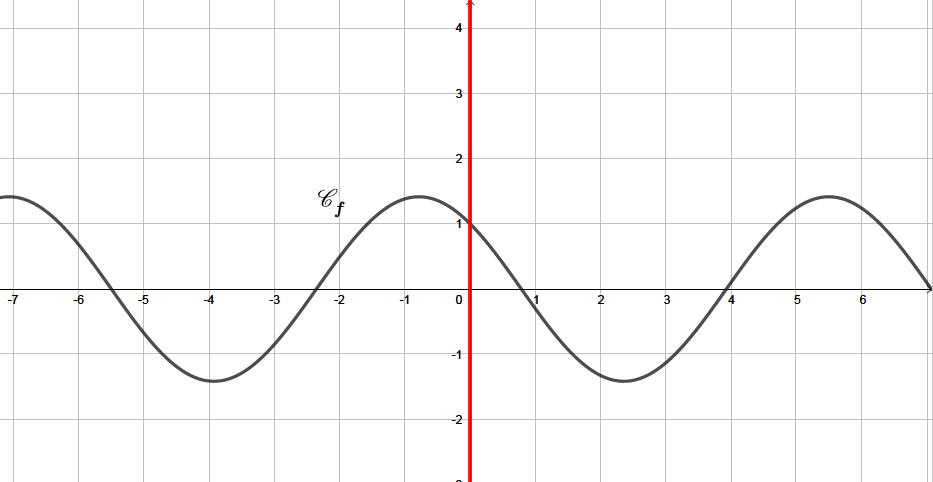
Question 5
Correction
est une fonction paire si pour tout réel , on a .
La fonction cosinus est paire.
est une fonction impaire si pour tout réel , on a .
La fonction sinus est impaire.
Attention, une fonction non paire n'est pas obligatoirement impaire et une fonction non impaire n'est pas obligatoirement paire.
Une fonction peut être ni paire, ni impaire.
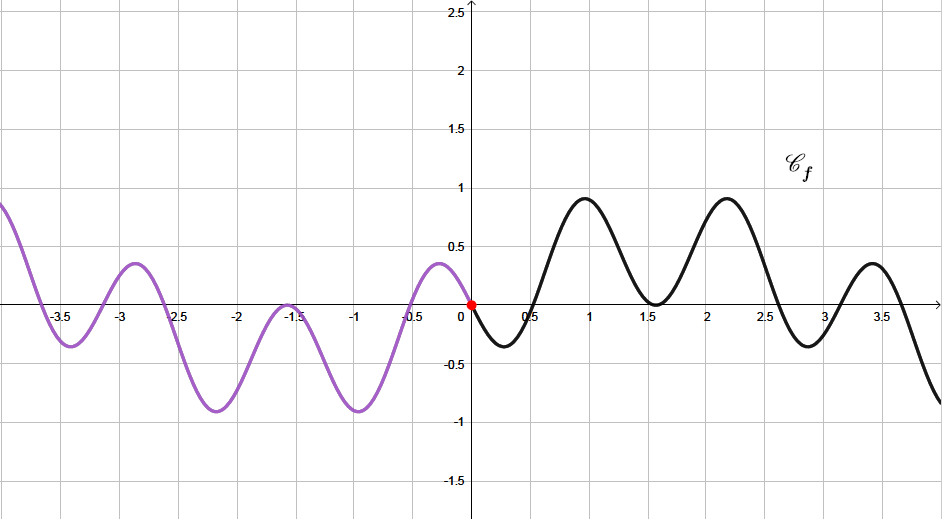
La fonction est une fonction impaire.
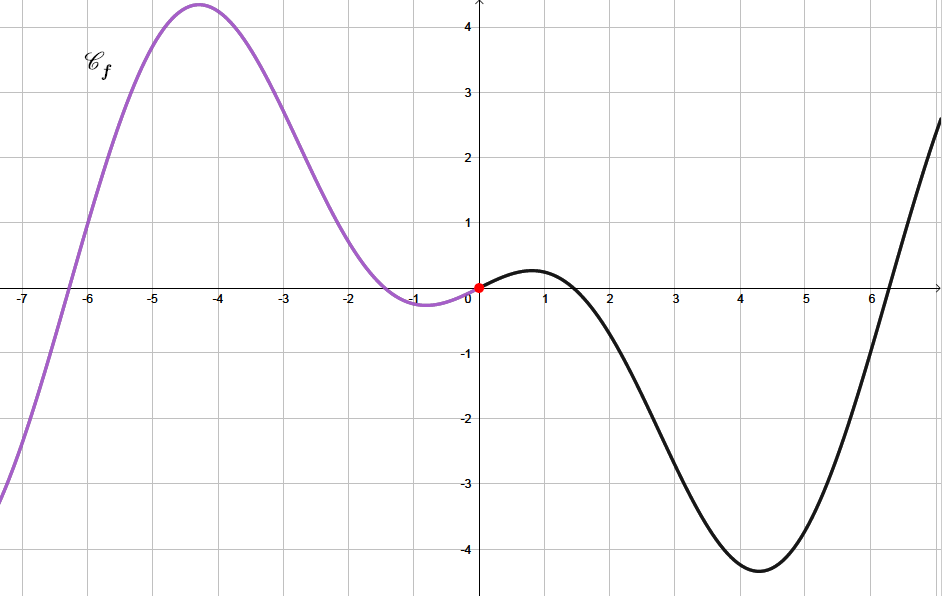
Question 6
Correction
est une fonction paire si pour tout réel , on a .
La fonction cosinus est paire.
est une fonction impaire si pour tout réel , on a .
La fonction sinus est impaire.
Attention, une fonction non paire n'est pas obligatoirement impaire et une fonction non impaire n'est pas obligatoirement paire.
Une fonction peut être ni paire, ni impaire.
La fonction est une fonction impaire.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.