Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Montrer que deux plans sont parallèles - Exercice 2

10 min
15
Question 1
Dans l'espace muni d'un repère (0;i→;j→;k→)\left(0;\overrightarrow{i} ;\overrightarrow{j} ;\overrightarrow{k} \right), on considère les deux plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) admettant pour équation cartésienne
(P1):x−y+2z−1=0\left(P_{1} \right):x-y+2z-1=0 et (P2):−2x+2y−4z+1=0\left(P_{2} \right):-2x+2y-4z+1=0

(P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont-ils parallèles ? Si oui, sont-ils également confondus ?

Correction
    Soient n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } des vecteurs normaux respectifs des plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right).
  • si n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } sont colinéaires alors (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont parallèles.
  • si n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } ne sont pas colinéaires alors (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) ne sont pas parallèles.
  • Dans le cas où les plans (P1):ax+by+cz+d=0\left(P_{1} \right):ax+by+cz+d=0 et (P2):a′x+b′y+c′z+d′=0\left(P_{2} \right):a'x+b'y+c'z+d'=0 sont parallèles il suffit de vérifier que les rapports aa′\frac{a}{a'} ; bb′\frac{b}{b'} ; cc′\frac{c}{c'} et dd′\frac{d}{d'} sont égaux. Dans ce cas les plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont confondus.
Soient n1→(1−12)\overrightarrow{n_{1} } \left(\begin{array}{c} {1} \\ {-1} \\ {2} \end{array}\right) et n2→(−22−4)\overrightarrow{n_{2} } \left(\begin{array}{c} {-2} \\ {2} \\ {-4} \end{array}\right) des vecteurs normaux respectifs des plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right).
On vérifie facilement que les deux vecteurs normaux sont colinéaires car :
n2→=−2×n1→\overrightarrow{n_{2} }=-2\times \overrightarrow{n_{1} }
, alors les plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont parallèles.
Maintenant, vérifions si les plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont confondus.
On calcule les rapports aa′\frac{a}{a'} ; bb′\frac{b}{b'} ; cc′\frac{c}{c'} et dd′\frac{d}{d'} .
On a aa′=1−2\frac{a}{a'} =\frac{1}{-2} ; bb′=−12\frac{b}{b'} =\frac{-1}{2} ; cc′=2−4=−12\frac{c}{c'} =\frac{2}{-4} =\frac{-1}{2} et dd′=−11\frac{d}{d'} =\frac{-1}{1}
Les rapports ne sont pas tous égaux donc les plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) ne sont pas confondus. Il sont juste parallèles comme indiqué précédemment.
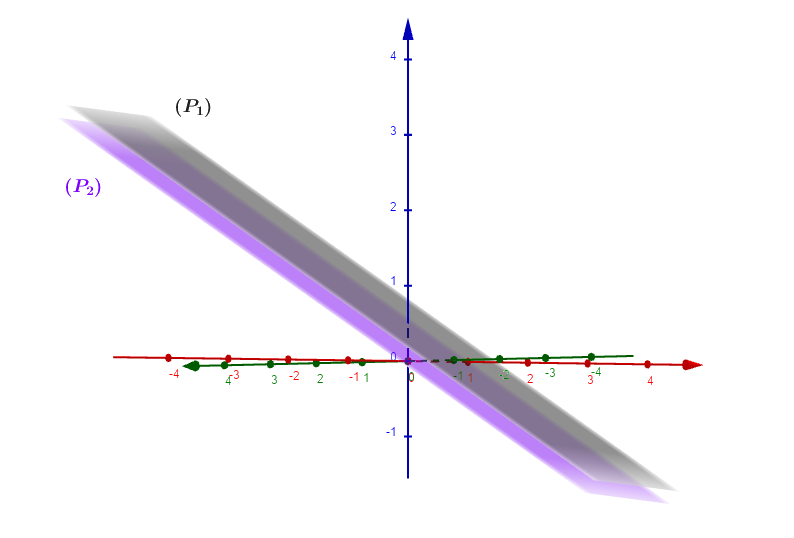
Question 2
Dans l'espace muni d'un repère (0;i→;j→;k→)\left(0;\overrightarrow{i} ;\overrightarrow{j} ;\overrightarrow{k} \right), on considère les deux plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) admettant pour équation cartésienne
(P1):2x−4y+6z−8=0\left(P_{1} \right):2x-4y+6z-8=0 et (P2):−x+2y−3z+4=0\left(P_{2} \right):-x+2y-3z+4=0

(P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont-ils parallèles ? Si oui, sont-ils également confondus ?

Correction
    Soient n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } des vecteurs normaux respectifs des plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right).
  • si n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } sont colinéaires alors (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont parallèles.
  • si n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } ne sont pas colinéaires alors (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) ne sont pas parallèles.
  • Dans le cas où les plans (P1):ax+by+cz+d=0\left(P_{1} \right):ax+by+cz+d=0 et (P2):a′x+b′y+c′z+d′=0\left(P_{2} \right):a'x+b'y+c'z+d'=0 sont parallèles il suffit de vérifier que les rapports aa′\frac{a}{a'} ; bb′\frac{b}{b'} ; cc′\frac{c}{c'} et dd′\frac{d}{d'} sont égaux. Dans ce cas les plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont confondus.
Soient n1→(2−46)\overrightarrow{n_{1} } \left(\begin{array}{c} {2} \\ {-4} \\ {6} \end{array}\right) et n2→(−12−3)\overrightarrow{n_{2} } \left(\begin{array}{c} {-1} \\ {2} \\ {-3} \end{array}\right) des vecteurs normaux respectifs des plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right).
On vérifie facilement que les deux vecteurs normaux sont colinéaires car :
n1⃗=−2×n2⃗\vec{n_{1} }=-2\times \vec{n_{2} }
, alors les plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont parallèles.
Maintenant, vérifions si les plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont confondus.
On calcule les rapports aa′\frac{a}{a'} ; bb′\frac{b}{b'} ; cc′\frac{c}{c'} et dd′\frac{d}{d'} .
On a aa′=2−1\frac{a}{a'} =\frac{2}{-1} ; bb′=−42\frac{b}{b'} =\frac{-4}{2} ; cc′=6−3\frac{c}{c'} =\frac{6}{-3} et dd′=−84\frac{d}{d'} =\frac{-8}{4}
Les rapports sont tous égaux donc les plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont confondus.