Exercices types : $$2$$^ère partie - Exercice 1

Notons $$D=\text{PGCD}\left(4n^{2}+7;2n^{2}+1\right)$$
$$D$$ divise $$4n^{2}+7$$ et $$D$$ divise $$2n^{2}+1$$ donc $$D$$ divise toute combinaison linéaire de $$4n^{2}+7$$ et $$2n^{2}+1$$ . Ainsi
$$D$$ divise $$\left(\blue{1}\times \left(4n^{2}+7\right)+\purple{\left(-2\right)}\times\left(2n^{2}+1\right)\right)$$ . Ici, nous avons construit une $$\red{\text{combinaison linéaire indépendante de}}$$ $$\red{n}$$
$$D$$ divise $$\left(4n^{2}+7-4n^{2}-2\right)$$
$$D$$ divise $$5$$
Il en résulte donc que le $$\text{PGCD}\left(a;b\right)$$ est bien un diviseur de $$5$$ .

Si $$\text{PGCD}\left(a;b\right)=5$$ alors $$a$$ est divisible par $$5$$ et $$b$$ et divisible par $$5$$.
Il en résulte donc que $$2n^{2}+1$$ est divisible par $$5$$.
Il existe donc un entier naturel $$k$$ tel que $$2n^{2}+1=5k$$ .

Nous allons dresser la table des restes modulo $$5$$ de $$2n^{2}+1$$.
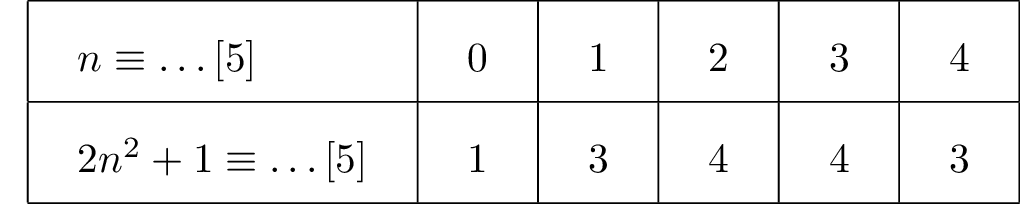D'après la table des restes modulo $$5$$, on peut affirmer que dans la division euclidienne de $$2n^{2}+1$$ par $$5$$, le reste est non nul .
Autrement dit, $$2n^{2}+1$$ n'est donc pas divisible par $$5$$ .

D'après la question $$1$$, nous avons vu que le $$\text{PGCD}\left(a;b\right)$$ est un diviseur de $$5$$ .
Les diviseurs de $$5$$ sont $$5$$ et $$1$$.
D'après la question $$3$$, nous avons démontré que $$\text{PGCD}\left(a;b\right)\ne5$$
Finalement, $$\text{PGCD}\left(a;b\right)=1$$ ce qui permet de conclure que $$a$$ et $$b$$ sont premiers entre eux.