Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Résoudre : et Ensembles de points : Cercle ou médiatrice - Exercice 1
15 min
20
Question 1
Dans chacun des cas suivants, déterminez l'ensemble des points du plan complexe dont l'affixe vérifie la condition donnée.
Regardez la vidéo Cercle et Médiatrice pour vous aider.
Regardez la vidéo Cercle et Médiatrice pour vous aider.
Correction
Soit le point d'affixe .
On pose ainsi
Il en résulte que
L'ensemble des points du plan tel que est le cercle de centre et de rayon .
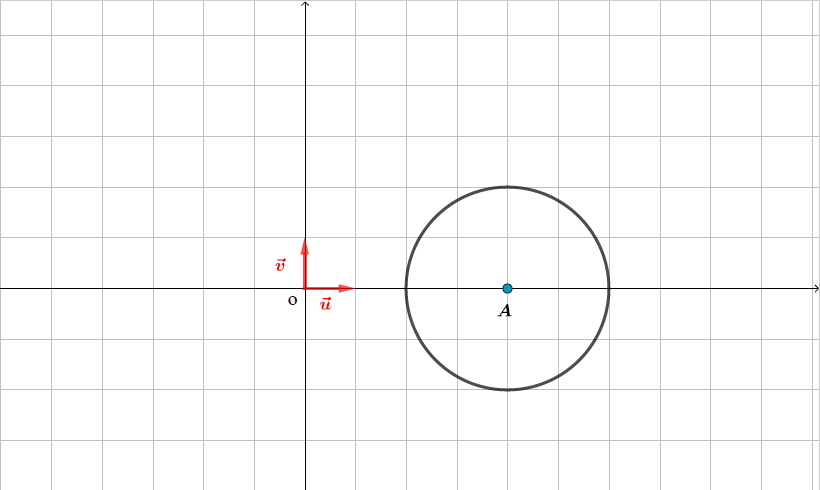
On pose ainsi
Il en résulte que
L'ensemble des points du plan tel que est le cercle de centre et de rayon .

Question 2
Correction
Soit le point d'affixe .
On pose ainsi
Il en résulte que
L'ensemble des points du plan tel que est le cercle de centre et de rayon .
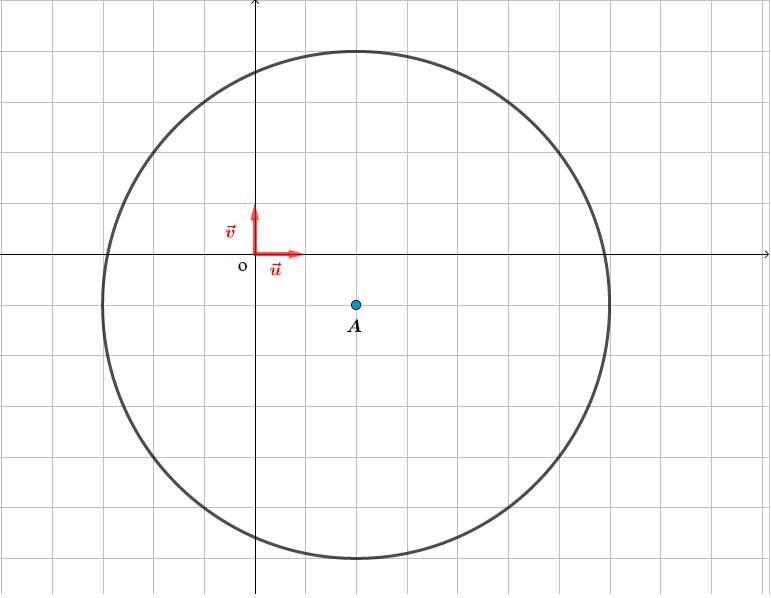
On pose ainsi
Il en résulte que
L'ensemble des points du plan tel que est le cercle de centre et de rayon .

Question 3
Correction
Nous allons commencer par calculer le module de .
Ainsi :
On pose ainsi
Il en résulte que
L'ensemble des points du plan tel que est le cercle de centre et de rayon .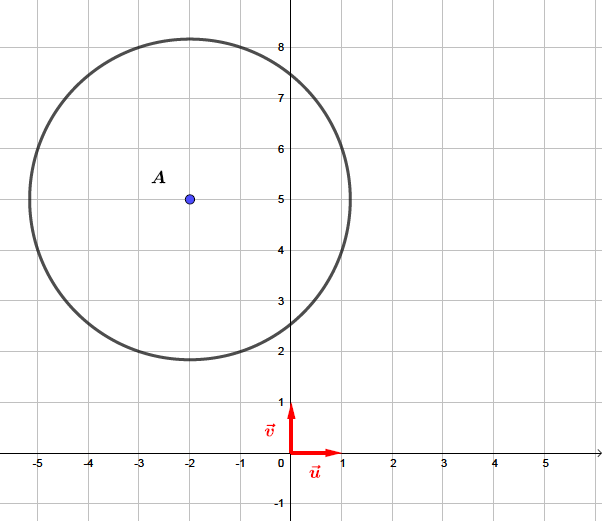
Ainsi :
On pose ainsi
Il en résulte que
L'ensemble des points du plan tel que est le cercle de centre et de rayon .

Question 4
Correction
Soit le point d'affixe .
On pose et ainsi
Il en résulte que
L'ensemble des points du plan tel que est la médiatrice du segment
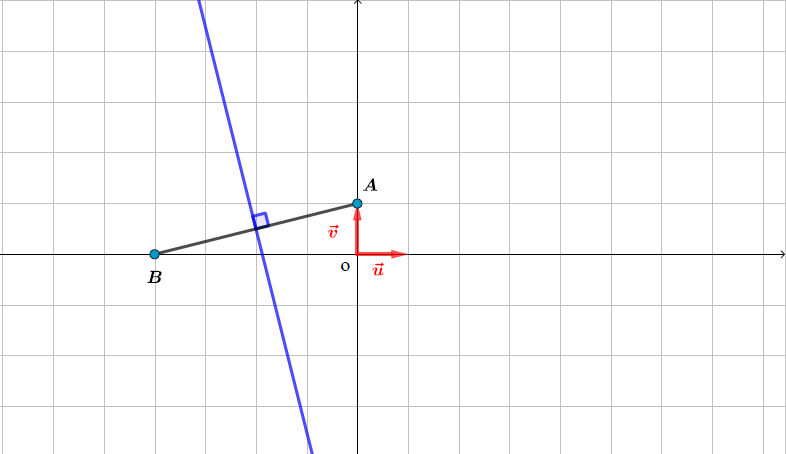
On pose et ainsi
Il en résulte que
L'ensemble des points du plan tel que est la médiatrice du segment

Question 5
Correction
Soit le point d'affixe .
On pose et ainsi
Il en résulte que
L'ensemble des points du plan tel que est la médiatrice du segment
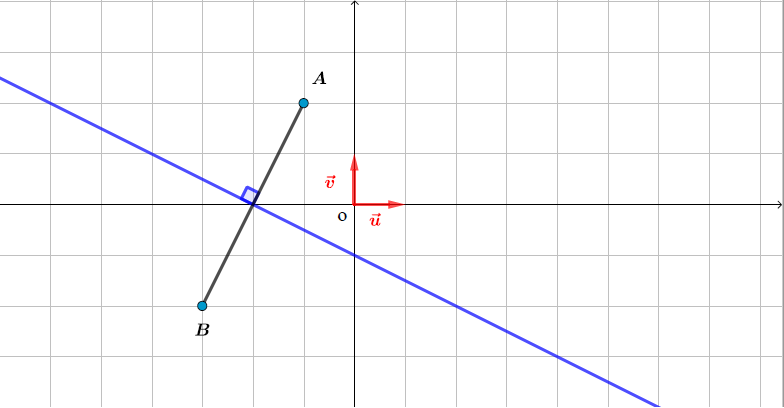
On pose et ainsi
Il en résulte que
L'ensemble des points du plan tel que est la médiatrice du segment

Question 6
Correction
Soit le point d'affixe .
équivaut successivement à :
On pose et ainsi
Il en résulte que
L'ensemble des points du plan tel que est la médiatrice du segment .
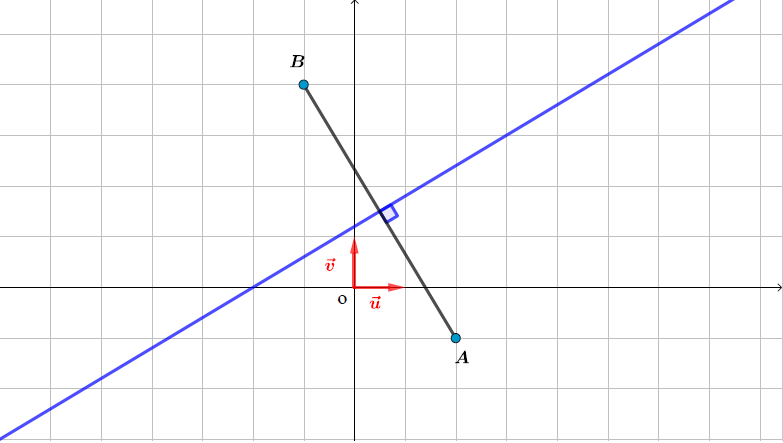
On pose et ainsi
Il en résulte que
L'ensemble des points du plan tel que est la médiatrice du segment .
