Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Nombres complexes et géométrie sous formes de problèmes - Exercice 1
10 min
15
On considère les points et d'affixes respectifs , ,
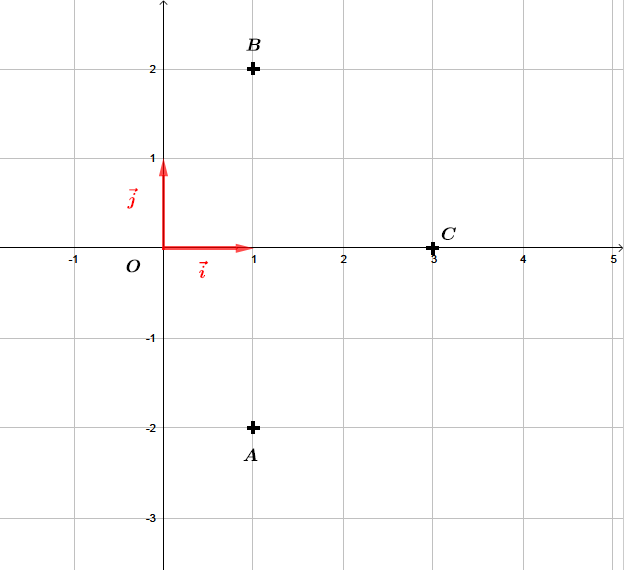
Question 1
Calculer .
Correction
Ainsi :
Question 2
En déduire la nature du triangle .
Correction
Comme , nous pouvons en déduire deux choses.
donc
ainsi
d'où
Le triangle est donc isocèle en .
ainsi
Le triangle est donc rectangle en .
Finalement, le triangle est un triangle rectangle isocèle en .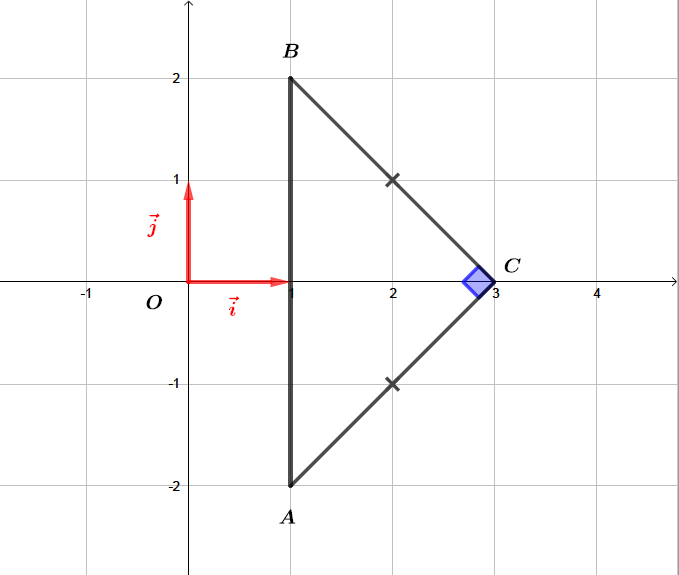
donc
ainsi
d'où
Le triangle est donc isocèle en .
.
Autrement dit, si est un imaginaire pur dont la partie imaginaire est positive alors l'argument de sera égale à
est un imaginaire pur dont la partie imaginaire est positive , donc d'après le rappel, on a : Autrement dit, si est un imaginaire pur dont la partie imaginaire est positive alors l'argument de sera égale à
ainsi
Soient , et trois points d'affixe respective , et tel que
Si ou si alors est un triangle rectangle en .
Soit Le triangle est donc rectangle en .
Finalement, le triangle est un triangle rectangle isocèle en .
