Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ère partie - Exercice 1
30 min
50
On considère l’équation ayant pour inconnue le nombre complexe .
Question 1
Pour tout nombre complexe , démontrer que
Correction
Il nous faut développer .
Question 2
Résoudre l'équation .
Correction
On considère l’équation que nous pouvons écrire
D'après la question , nous savons que .
Il en résulte donc que résoudre l'équation revient à résoudre
Ainsi :
C'est une équation produit nul donc ou
alors .
, il existe donc deux racines complexes conjuguées notées et tels que et
et
et
Ainsi :
Donc
D'après la question , nous savons que .
Il en résulte donc que résoudre l'équation revient à résoudre
Ainsi :
C'est une équation produit nul donc ou
alors .
, il existe donc deux racines complexes conjuguées notées et tels que et
et
et
Ainsi :
et
Donc
Question 3
Écrire les solutions de l’équation sous forme exponentielle.
Correction
D'après la question , nous savons que les solutions de l'équation sont .
on note
Pour l'argument on sait que
On a donc
d'où
Avec le cercle trigonométrique on en déduit que
Ainsi
on note
Pour l'argument on sait que
Ainsi :
Avec le cercle trigonométrique on en déduit que
Ainsi
on note
On remarque que est le conjugué de .
Il en résulte donc que :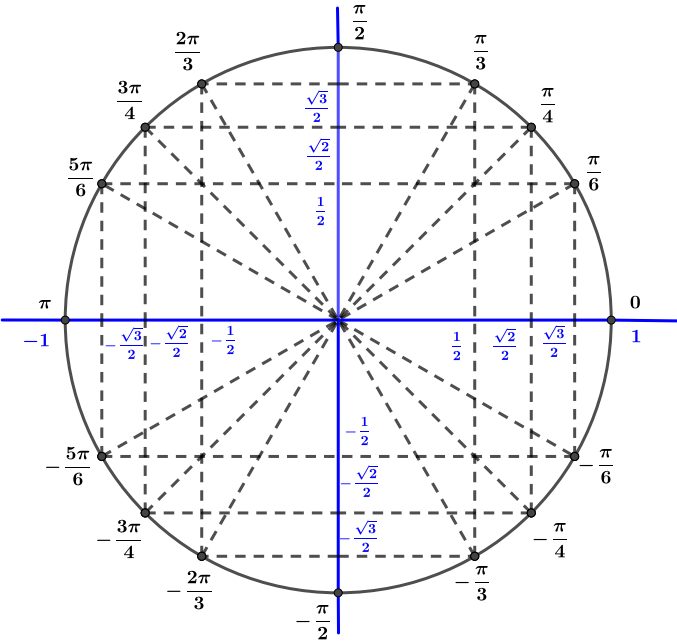
on note
Pour l'argument on sait que
On a donc
d'où
Avec le cercle trigonométrique on en déduit que
Ainsi
on note
Pour l'argument on sait que
Ainsi :
Avec le cercle trigonométrique on en déduit que
Ainsi
on note
On remarque que est le conjugué de .
Il en résulte donc que :

Question 4
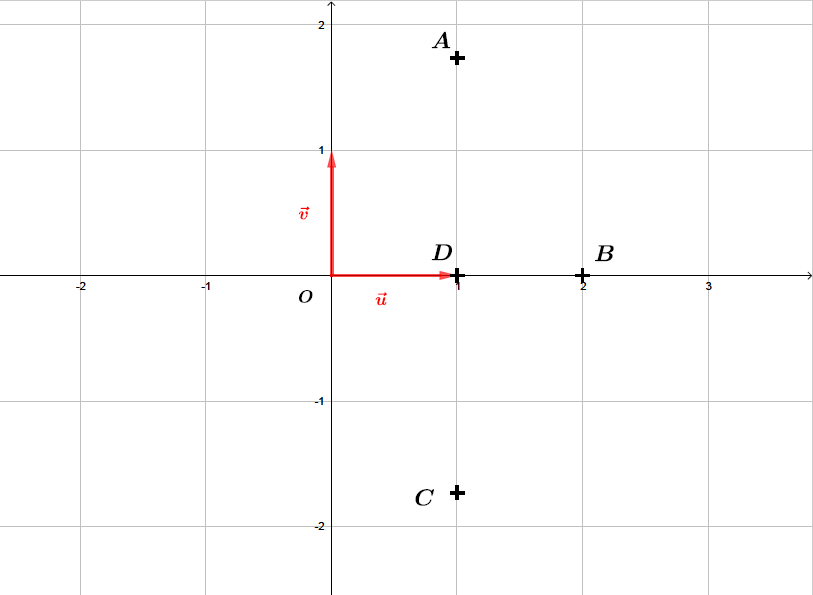
On munit le plan complexe d’un repère orthonormé direct .
Soient et les quatre points d’affixes respectives ; ; et .
Soient et les quatre points d’affixes respectives ; ; et .
Faire une figure.
Correction
Question 5
Quelle est la nature du quadrilatère ? Justifier.
Correction
On conjecture que le quadrilatère est un losange. Il faut donc montrer que est un parallélogramme avec deux cotés consécutifs égaux.
est un parallélogramme si et seulement si .
Nous avons bien . il en résulte que le quadrilatère est un parallélogramme.
Calculons maintenant les mesures des cotés et .
Finalement, est un parallélogramme avec deux cotés consécutifs égaux. Autrement dit, est un losange.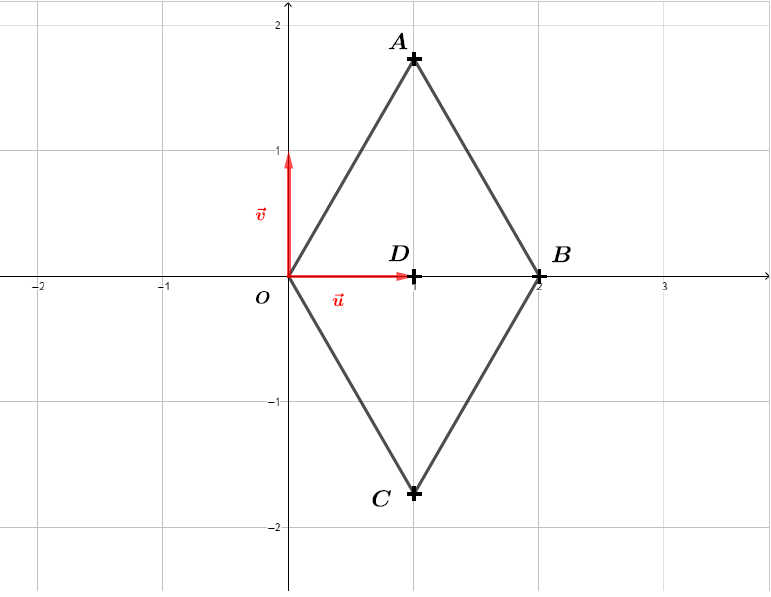
- Si et sont les affixes respectives des points et dans un repère orthonormé, alors l'affixe du vecteur est égale à .
Nous avons bien . il en résulte que le quadrilatère est un parallélogramme.
Calculons maintenant les mesures des cotés et .

Question 6
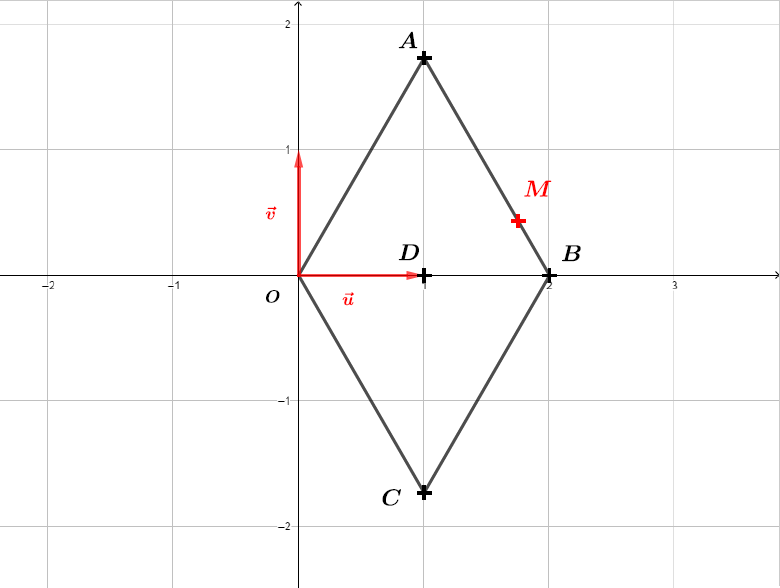
Soit le point d’affixe .
Démontrer que les points et sont alignés.
Correction
- Si et sont les affixes respectives des points et dans un repère orthonormé, alors l'affixe du vecteur est égale à .
On remarque que :
Les vecteurs et sont donc les points et sont alignés.
Question 7
Démontrer que le triangle est rectangle.
Correction
On conjecture que le triangle est rectangle en .
La est égale à
et que
D'après la réciproque du théorème de Pythagore, le triangle est rectangle en .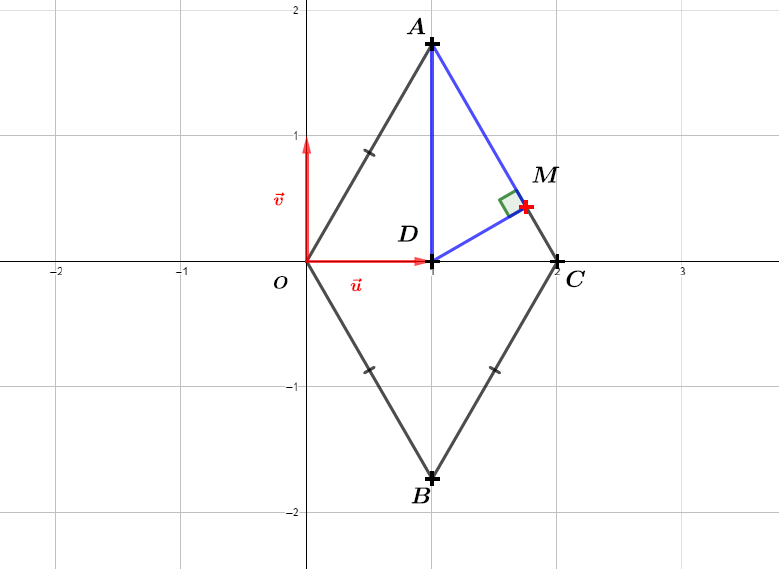
- Soient et deux points d'affixe respective et .
et que
D'après la réciproque du théorème de Pythagore, le triangle est rectangle en .
