Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie - Exercice 1
5 min
15
Question 1
Déterminer les valeurs de pour lesquelles est divisible par .
Correction
Dans un premier temps, il nous faut déterminer les restes de la division euclidienne de par .
Les restes possibles dans la division euclidienne de par sont :
Maintenant, en utilisant un tableau des congruences modulo , nous allons déterminer les valeurs de pour lesquelles est divisible par .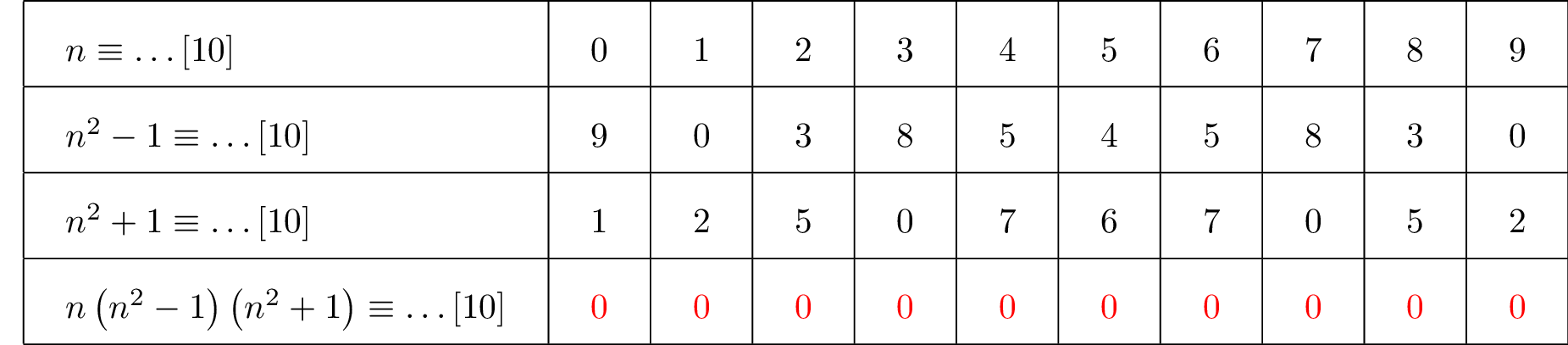 est divisible par si l'on peut écrire : .
est divisible par si l'on peut écrire : .
D'après le tableau des congruences modulo cela est vrai pour toutes les valeurs de .
On peut alors conclure que est divisible par pour tout entier naturel .
Soit un entier relatif et un entier naturel non nul.
On appelle division euclidienne de par , l’opération qui au couple associe le couple tel que : avec s’appelle le dividende, le diviseur, le quotient et le reste.
Nous avons : avec Les restes possibles dans la division euclidienne de par sont :
Maintenant, en utilisant un tableau des congruences modulo , nous allons déterminer les valeurs de pour lesquelles est divisible par .

D'après le tableau des congruences modulo cela est vrai pour toutes les valeurs de .
On peut alors conclure que est divisible par pour tout entier naturel .