Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Congruences et équations - Exercice 1
8 min
15
Question 1
Soit un entier naturel, résoudre
Correction
Les restes de la division euclidienne par sont et .
Maintenant, en utilisant un tableau des congruences modulo , on obtient :
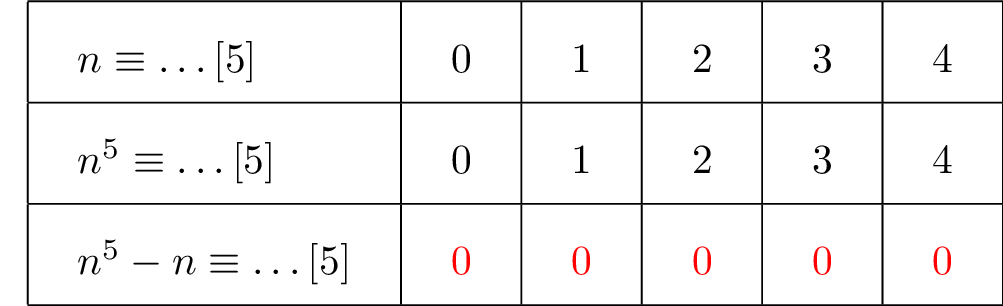 Il faut analyser la dernière ligne de ce tableau de congruence.
Il faut analyser la dernière ligne de ce tableau de congruence.
Cela signifie que quel que soit l'entier naturel , est divisible par . En effet, il n'y a que des zéros à la dernière ligne qui confirme l'écriture .
Autrement dit, tous les entiers naturels vérifient
Maintenant, en utilisant un tableau des congruences modulo , on obtient :

Cela signifie que quel que soit l'entier naturel , est divisible par . En effet, il n'y a que des zéros à la dernière ligne qui confirme l'écriture .
Autrement dit, tous les entiers naturels vérifient
Question 2
Soit un entier naturel, résoudre
Correction
Les restes de la division euclidienne par sont et .
Maintenant, en utilisant un tableau des congruences modulo , on obtient : Il faut analyser la dernière ligne de ce tableau de congruence.
Il faut analyser la dernière ligne de ce tableau de congruence.
Cela signifie que quel que soit l'entier naturel , est divisible par . En effet, il n'y a que des zéros à la dernière ligne qui confirme l'écriture .
Autrement dit, tous les entiers naturels vérifient
Maintenant, en utilisant un tableau des congruences modulo , on obtient :

Cela signifie que quel que soit l'entier naturel , est divisible par . En effet, il n'y a que des zéros à la dernière ligne qui confirme l'écriture .
Autrement dit, tous les entiers naturels vérifient
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.