Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Matrices et transformations géométriques dans le plan : L'homothétie - Exercice 1

4 min
10
Question 1

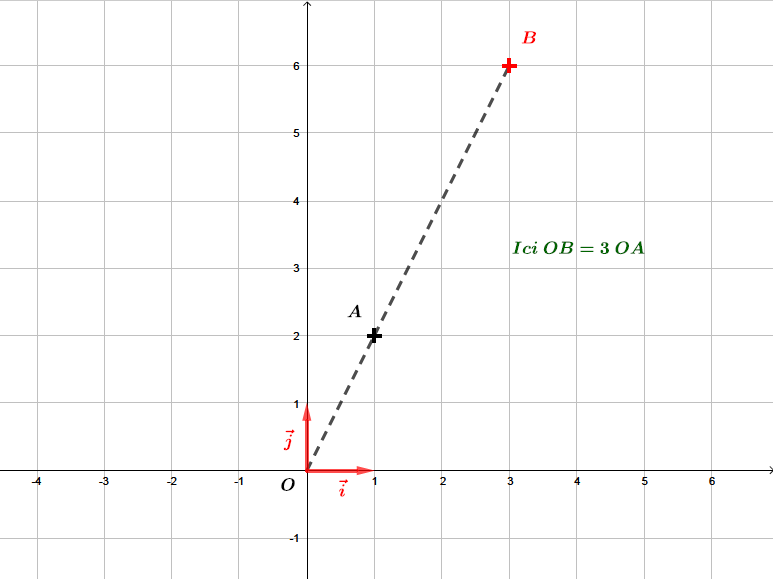
Dans un repère orthonormé direct (O;i→;j→)\left(O;\overrightarrow{i} ;\overrightarrow{j} \right), on donne le point A(1;2)A\left(1;2\right) .
Déterminer les coordonnées du point BB image du point AA par l'homothétie de centre OO et de rapport 33 .

Correction
On se place dans un repère orthonormé direct (O;i→;j→)\left(O;\overrightarrow{i} ;\overrightarrow{j} \right) du plan.
  • Soient A(xA;yA)A\left(x_{A}; y_{A}\right) et B(xB;yB)B\left(x_{B}; y_{B}\right) deux points du plan et kk un réel.
  • BB est l'image de AA par l’homotheˊtie \red{\text{l'homothétie }} de centre OO et de rapport kk si et seulement si (xByB)=(k00k)×(xAyA)\left(\begin{array}{c} {x_{B} } \\ {y_{B} } \end{array}\right)=\left(\begin{array}{cc} {k} & {0} \\ {0} & {k} \end{array}\right)\times \left(\begin{array}{c} {x_{A} } \\ {y_{A} } \end{array}\right)
    • La matrice associée à l'homothétie de centre OO et de rapport 33 est : (3003)\left(\begin{array}{cc} {3} & {0} \\ {0} & {3} \end{array}\right)
    Nous appliquons la formule du rappel, il vient alors que :
    (xByB)=(3003)×(12)\left(\begin{array}{c} {x_{B} } \\ {y_{B} } \end{array}\right)=\left(\begin{array}{cc} {{\color{blue}{3}}} & {{\color{blue}{0}}} \\ {{\color{red}{0}}} & {{\color{red}{3}}} \end{array}\right)\times \left(\begin{array}{c} {{\color{green}{1}} } \\ {{\color{green}{2}} } \end{array}\right)
    (xByB)=(3×1+0×20×1+3×2)\left(\begin{array}{c} {x_{B} } \\ {y_{B} } \end{array}\right)=\left(\begin{array}{c} {{\color{blue}{3}}\times {\color{green}{1}}+{\color{blue}{0}}\times {\color{green}{2}}} \\ {{\color{red}{0}}\times \color{green}{1}+{\color{red}{3}}\times 2} \end{array}\right)
    (xByB)=(3+00+6)\left(\begin{array}{c} {x_{B} } \\ {y_{B} } \end{array}\right)=\left(\begin{array}{c} {3+0} \\ {0+6} \end{array}\right)
    Ainsi :
    (xByB)=(36)\left(\begin{array}{c} {x_{B} } \\ {y_{B} } \end{array}\right)=\left(\begin{array}{c} {3} \\ {6} \end{array}\right)

    Les coordonnées du point BB image du point AA par l'homothétie de centre OO et de rapport 33 sont B(3;6)B\left(3;6\right)