Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Probabilités conditionnelles et indépendance : Rappels\red{\text{Rappels}} - Exercice 1

7 min
10
On considère deux évènements AA et BB associées à une expérience aléatoire modélisée par l'arbre pondéré ci-dessous :
Question 1

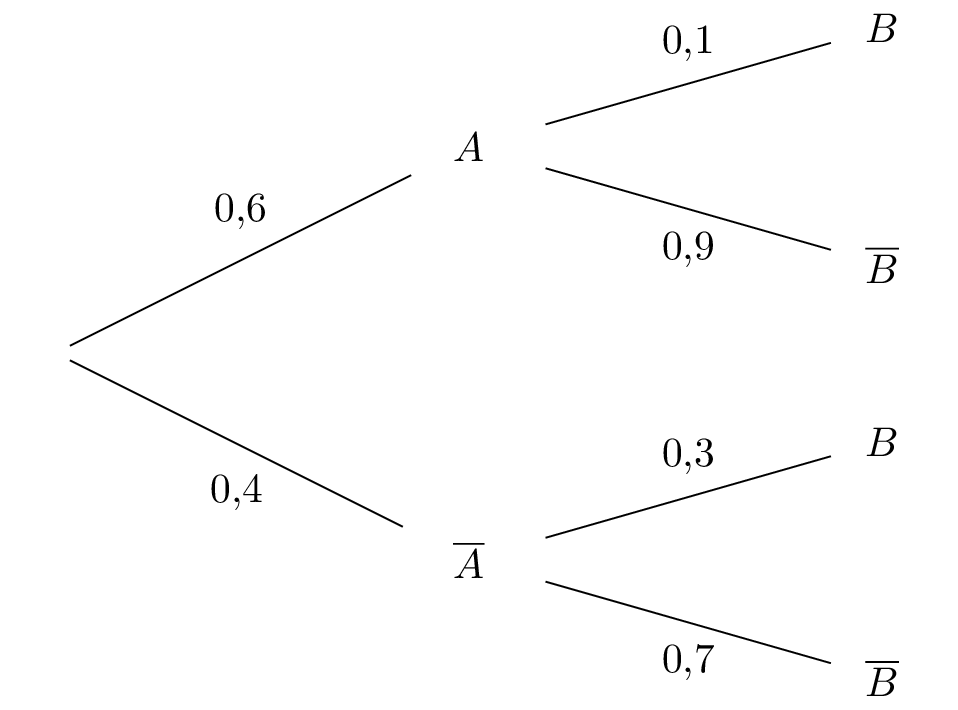
Donner à l'aide de l'arbre pondéré les valeurs de PA(B)P_{A} \left(B\right) et PA‾(B‾)P_{\overline{A}} \left(\overline{B}\right)

Correction
Nous pouvons lire que :
  • PA(B)=0,1P_{A} \left(B\right)=0,1
  • PA‾(B‾)=0,7P_{\overline{A}} \left(\overline{B}\right)=0,7
    • Question 2

    Calculer P(A∩B)P\left(A\cap B\right)

    Correction
    L’événement A∩BA\cap B correspond à l’événement AA et{\color{blue}{\text{et}}} à l’événement BB.
    P(A∩B)=P(A)×PA(B)P\left(A\cap B\right)=P\left(A\right)\times P_{A} \left(B\right)
    P(A∩B)=0,6×0,1P\left(A\cap B\right)=0,6\times 0,1
    Ainsi :
    P(A∩B)=0,06P\left(A\cap B\right)=0,06

    Question 3

    Déterminer la probabilité de l'évènement P(B)P\left(B\right) .

    Correction
    AA et A‾\overline{A} forment une partition de l'univers.
    D'après la formule des probabilités totales on a :
    P(B)=P(A∩B)+P(A‾∩B)P\left(B\right)=P\left(A\cap B\right)+P\left(\overline{A}\cap B\right)
    P(B)=P(A)×PA(B)+P(A‾)×PA‾(B)P\left(B\right)=P\left(A\right)\times P_{A} \left(B\right)+P\left(\overline{A}\right)\times P_{\overline{A}} \left(B\right)
    Soit : P(B)=0,6×0,1+0,4×0,3P\left(B\right)=0,6\times 0,1 +0,4\times 0,3
    Ainsi :
    P(B)=0,18P\left(B\right)=0,18

    Question 4

    Calculer PB(A‾)P_{B} \left(\overline{A}\right)

    Correction
      On note PB(A)P_{B} \left(A\right) la probabilité d’avoir l’événement AA sachant que l’événement BB est réalisé. On a alors la relation suivante :
    • PB(A)=P(A∩B)P(B)P_{B} \left(A\right)=\frac{P\left(A\cap B\right)}{P\left(B\right)}
    Il vient alors que :
    PB(A‾)=P(A‾∩B)P(B)P_{B} \left(\overline{A}\right)=\frac{P\left(\overline{A}\cap B\right)}{P\left(B\right)}
    PB(A‾)=P(A‾)×PA‾(B)P(B)P_{B} \left(\overline{A}\right)=\frac{P\left(\overline{A}\right)\times P_{\overline{A}} \left(B\right)}{P\left(B\right)} . D'après la question 33, nous savons que P(B)=0,18P\left(B\right)=0,18
    Ainsi : PB(A‾)=0,4×0,30,18P_{B} \left(\overline{A}\right)=\frac{0,4\times 0,3}{0,18}
    d'où :
    PB(A‾)=23P_{B} \left(\overline{A}\right)=\frac{2}{3}

    Question 5

    Les évènements AA et BB sont-ils indépendants ?

    Correction
      Deux événements AA et BB sont indépendants si et seulement si :
    • P(A∩B)=P(A)×P(B)P\left(A\cap B\right)=P\left(A\right) \times P\left(B\right)
  • D'après la question 22, nous savons que P(A∩B)=0,06P\left(A\cap B\right)=0,06
    • Il nous reste donc à calculer P(A)×P(B)P\left(A\right) \times P\left(B\right).
  • D'après la question 33, nous savons que P(B)=0,18P\left(B\right)=0,18 et d'après l'arbre pondéré nous pouvons lire que P(A)=0,6P\left(A\right)=0,6
    • Il vient que :
    P(A)×P(B)=0,6×0,18P\left(A\right) \times P\left(B\right)=0,6 \times 0,18
    P(A)×P(B)=0,108P\left(A\right) \times P\left(B\right)=0,108
    Finalement :
    P(A∩B)≠P(A)×P(B)P\left(A\cap B\right){\color{red}{\ne}} P\left(A\right) \times P\left(B\right)
    Les événements AA et BB ne sont donc pas indeˊpendants\text{\blue{ne sont donc pas indépendants}}.