Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →

Tchat avec un prof

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →

Exercices types : $1$ ^ère partie - Exercice 1

25 min

On étudie certaines caractéristiques d’un supermarché d’une petite ville.

Question 1

Partie A-Démonstration préliminaire.
Soit

X

une variable aléatoire qui suit la loi exponentielle de paramètre

0,2

. On rappelle que l’espérance de la variable aléatoire

X

, notée

E\left(X\right)

, est égale à :

\lim\limits_{x\to +\infty } \int _{0}^{x}0,2te^{-0,2t} dt

.
Le but de cette partie est de démontrer que

E\left(X\right)=5

On note $g$ la fonction définie sur l’intervalle $\left[0;+\infty\right[$ par $g\left(t\right)=0,2te^{-0,2t}$ . On définit la fonction $G$ sur l’intervalle $\left[0;+\infty\right[$ par $G\left(t\right)=\left(-t-5\right)e^{-0,2t}$ .
Vérifier que $G$ est une primitive de $g$ sur l’intervalle $\left[0;+\infty\right[$ .

Correction

Dans le cas où une primitive

F

est donnée, il vous suffit de dériver

F

et d'obtenir comme résultat

f

.
Autrement dit, il faut que

F'\left(x\right)=f\left(x\right)

Soit :

G\left(t\right)=\left(-t-5\right)e^{-0,2t}

On reconnaît la forme :

\left(uv\right)'=u'v+uv'

avec

u\left(t\right)=-t-5

v\left(t\right)=e^{-0,2t}

.
Ainsi :

u'\left(t\right)=-1

v'\left(t\right)=-0,2e^{-0,2t}

.
Il vient alors que :

G'\left(t\right)=-1\times e^{-0,2t} +\left(-t-5\right)\times \left(-0,2e^{-0,2t} \right)

G'\left(t\right)=e^{-0,2t} \left(-1+\left(-t-5\right)\times \left(-0,2\right)\right)

G'\left(t\right)=e^{-0,2t} \left(-1+\left(-t\right)\times \left(-0,2\right)+\left(-5\right)\times \left(-0,2\right)\right)

G'\left(t\right)=e^{-0,2t} \left(-1+0,2t+1\right)

G'\left(t\right)=0,2te^{-0,2t}

G'\left(t\right)=g\left(t\right)

La fonction

G

est donc bien une primitive de

g

sur

\left[0;+\infty\right[

Question 2

En déduire que la valeur exacte de $E\left(X\right)$ est $5$ . On pourra utiliser, sans le démontrer, le résultat suivant : $\lim\limits_{x\to +\infty }xe^{-0,2x}=0$ .

Correction

En appliquant la définition de l’espérance, rappelée dans l’énoncé, on va commencer par calculer l’intégrale de

g

entre

0

x

.
Il vient alors que :

\int _{0}^{x}0,2te^{-0,2t} dt= \int _{0}^{x}g\left(t\right)dt

\int _{0}^{x}0,2te^{-0,2t} dt= \left[G\left(t\right)\right]_{0}^{x}

\int _{0}^{x}0,2te^{-0,2t} dt= G\left(x\right)-G\left(0\right)

\int _{0}^{x}0,2te^{-0,2t} dt= \left(-x-5\right)e^{-0,2x} -\left(-0-5\right)e^{-0,2\times 0}

\int _{0}^{x}0,2te^{-0,2t} dt= \left(-x-5\right)e^{-0,2x} -\left(-5\right)e^{0}

Ainsi :

\int _{0}^{x}0,2te^{-0,2t} dt=-x e^{-0,2x} -5e^{-0,2x} +5

Il en résulte donc que :

\lim\limits_{x\to +\infty } \int _{0}^{x}0,2te^{-0,2t} dt =\lim\limits_{x\to +\infty }-x e^{-0,2x} -5e^{-0,2x} +5

Nous savons que

\lim\limits_{x\to +\infty }xe^{-0,2x}=0

. Il nous faut donc calculer maintenant

\lim\limits_{x\to +\infty }-5e^{-0,2x}=0

.
Ici, il s'agit d'une limite par composition.
On commence par calculer

\lim\limits_{x\to +\infty } -0,2x=-\infty

.
On pose

X=-0,2x

.
Ainsi :

\lim\limits_{X\to -\infty } -5e^{X} =0

.
Par composition :

\lim\limits_{x\to +\infty } 5e^{-0,2x} =0

Finalement :

\left. \begin{array}{ccc} {\lim\limits_{x\to +\infty } -x e^{-0,2x} } & {=} & {0 } \\ {\lim\limits_{x\to +\infty } -5e^{-0,2x} +5} & {=} & {5} \end{array}\right\}

par somme

\lim\limits_{x\to +\infty } \int _{0}^{x}0,2te^{-0,2t} dt =5

Question 3

Partie B- Durée d’attente pour le paiement.
Ce supermarché laisse le choix au client d’utiliser seul des bornes automatiques de paiement ou bien de passer par une caisse gérée par un opérateur.
La durée d’attente à une borne automatique, exprimée en minutes, est modélisée par une variable aléatoire qui suit la loi exponentielle de paramètre

0,2

minute.

Donner la durée moyenne d’attente d’un client à une borne automatique de paiement.

Correction

X

\lambda

$E\left( X\right)=\frac{1}{\lambda}$

Comme cette variable aléatoire suit la loi exponentielle de paramètre

0,2

minute. Cela signifie que

\lambda=0,2

.
Il vient alors que :

E\left(X\right)=\frac{1}{0,2} =5

Question 4

Calculer la probabilité, arrondie à $10^{-3}$ , que la durée d’attente d’un client à une borne automatique de paiement soit supérieure à $10$ minutes.

Correction

La fonction de densité de probabilité de la loi exponentielle sur

\left[0;+\infty \right[

est

f\left(x\right)=\lambda e^{-\lambda x}

où

\lambda

est un réel positif.

$P\left(a\le X\le b\right)=\int _{a}^{b}\lambda e^{-\lambda x} dx=\left[-e^{-\lambda x} \right] _{a}^{b} =e^{-\lambda a} -e^{-\lambda b}$
$P\left(X\le a\right)=P\left(0\le X\le a\right)=\int _{0}^{a}\lambda e^{-\lambda x} dx=\left[-e^{-\lambda x} \right] _{0}^{a} =1-e^{-\lambda a}$
$P\left(X\ge a\right)=1-P\left(X\le a\right)=1-\left(1-e^{-\lambda a} \right)=e^{-\lambda a}$

On a :

P\left(X\ge 10\right)=1-e^{-0,2\times10}

P\left(X\ge 10\right)\approx0,135

10^{-3}

, la probabilité qu’un client attende plus de dix minutes aux bornes automatiques est donc de

0,135

Question 5

L’étude commandée par le gérant conduit à la modélisation suivante :

parmi les clients ayant choisi de passer à une borne automatique,

86\%

attendent moins de

10

minutes;

parmi les clients passant en caisse,

63\%

attendent moins de

10

minutes.

On choisit un client du magasin au hasard et on définit les évènements suivants :

B

: « le client paye à une borne automatique » ;

\overline{B}

: « le client paye à une caisse avec opérateur »;

S

:« la durée d’attente du client lors du paiement est inférieure à

10

minutes».

Une attente supérieure à dix minutes à une caisse avec opérateur ou à une borne automatique engendre chez le client une perception négative du magasin. Le gérant souhaite que plus de $75\%$ des clients attendent moins de $10$ minutes. Quelle est la proportion minimale de clients qui doivent choisir une borne automatique de paiement pour que cet objectif soit atteint?

Correction

Nous ne connaissons pas la valeur de la probabilité de l'évènement

B

. Nous allons poser, un réel

p

tel que

P\left(B\right)=p

. Nous allons dresser un tableau pondéré traduisant la situation de l'énoncé. Il vient alors que :

B

\overline{B}

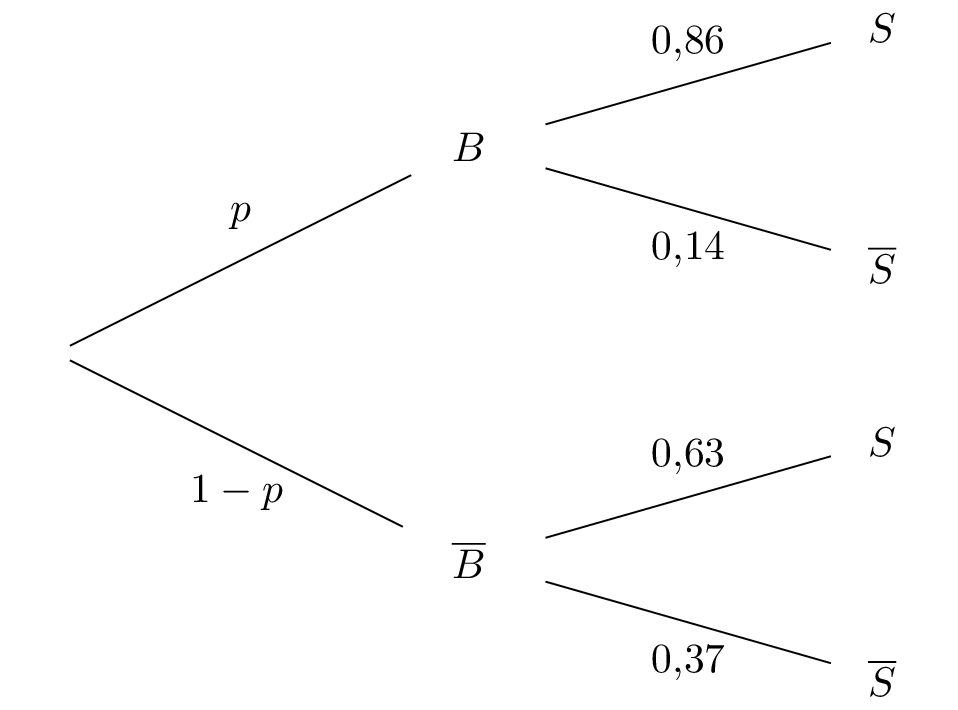forment une partition de l'univers.
D'après la formule des probabilités totales on a :

P\left(S\right)=P\left(B\cap S\right)+P\left(\overline{B}\cap S\right)

P\left(S\right)=P\left(B\right)\times P_{B} \left(S\right)+P\left(\overline{B}\right)\times P_{\overline{B}} \left(S\right)

Soit :

P\left(S\right)=p\times 0,86 +\left(1-p\right)\times 0,63

P\left(S\right)=0,86p +0,63-0,63p

Ainsi :

P\left(S\right)=0,23p+0,63

Pour que plus de

75\%

des clients attendent moins de dix minutes, on doit avoir :

P\left(S\right)\ge 0,75\Leftrightarrow 0,63+0,23p\ge 0,75

P\left(S\right)\ge 0,75\Leftrightarrow 0,23p\ge 0,75-0,63

P\left(S\right)\ge 0,75\Leftrightarrow 0,23p\ge 0,12

P\left(S\right)\ge 0,75\Leftrightarrow p\ge \frac{0,12}{0,23}

\frac{0,12}{0,23}\approx0,522

.
La proportion minimale de clients devant choisir les caisses automatiques, si on veut que plus de

75\%

des clients attendent moins de dix minutes est donc de

52,2\%

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.

Exercices types : 111ère partie - Exercice 1

En déduire que la valeur exacte de E(X)E\left(X\right)E(X) est 555. On pourra utiliser, sans le démontrer, le résultat suivant : lim⁡x→+∞xe−0,2x=0\lim\limits_{x\to +\infty }xe^{-0,2x}=0x→+∞lim​xe−0,2x=0.

Donner la durée moyenne d’attente d’un client à une borne automatique de paiement.

Calculer la probabilité, arrondie à 10−310^{-3}10−3, que la durée d’attente d’un client à une borne automatique de paiement soit supérieure à 101010 minutes.

Exercices types : $1$ ^ère partie - Exercice 1

En déduire que la valeur exacte de $E\left(X\right)$ est $5$ . On pourra utiliser, sans le démontrer, le résultat suivant : $\lim\limits_{x\to +\infty }xe^{-0,2x}=0$ .

Calculer la probabilité, arrondie à $10^{-3}$ , que la durée d’attente d’un client à une borne automatique de paiement soit supérieure à $10$ minutes.