Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Premier contact avec le théorème des valeurs intermédiaires - Exercice 2
5 min
10
Question 1
Soit une fonction continue sur l'intervalle . On dresse le tableau de variation ci-dessous :
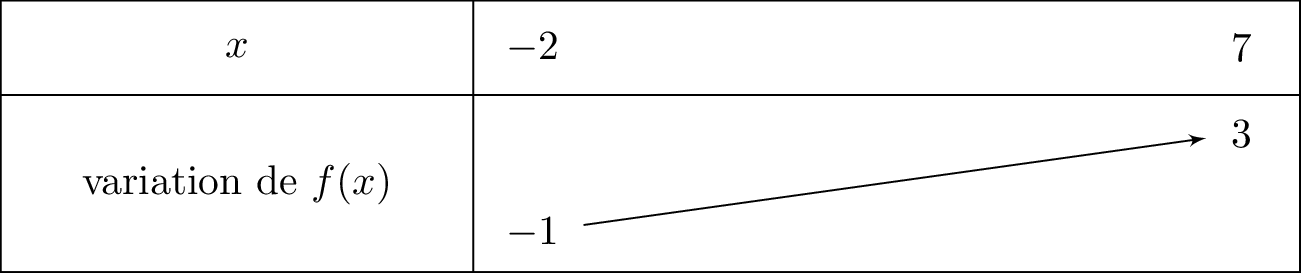

Démontrer que l'équation admet une unique solution sur .
On notera cette solution.
On notera cette solution.
Correction
Nous faisons apparaître le zéro recherché dans le tableau de variation donnée. Il vient alors que : 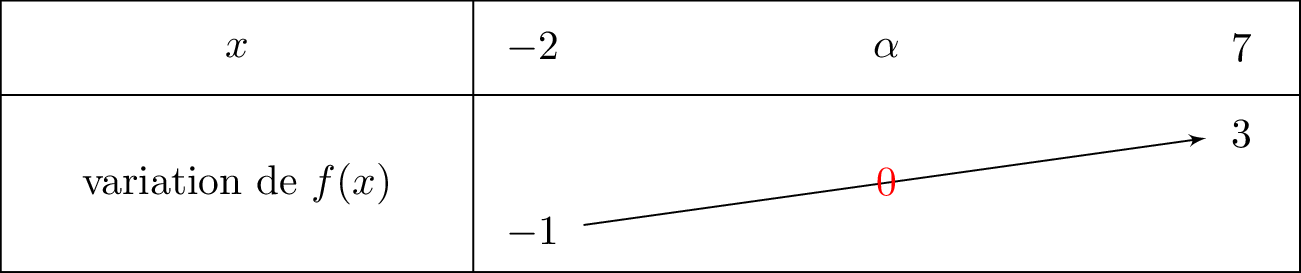 Sur , la fonction est et
Sur , la fonction est et
De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution appartenant à l'intervalle tel que .

De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution appartenant à l'intervalle tel que .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.