Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie - Exercice 2
20 min
35
Question 1
Soit une fonction définie sur par : et sa courbe représentative dans un repère du plan.
Déterminer la limite de la fonction en et en .
Correction
D'une part : . Au voisinage de , un polynôme est équivalent à son monôme de plus haut degré. Autrement dit, on n'étudie que la limite du monôme de plus haut degré.
Donc :
D'autre part : . Au voisinage de , un polynôme est équivalent à son monôme de plus haut degré. Autrement dit, on n'étudie que la limite du monôme de plus haut degré.
Donc :
Donc :
D'autre part : . Au voisinage de , un polynôme est équivalent à son monôme de plus haut degré. Autrement dit, on n'étudie que la limite du monôme de plus haut degré.
Donc :
Question 2
Déterminer le tableau de variation de la fonction sur .
Correction
est dérivable sur .
Ainsi : , il existe donc deux racines réelles distinctes telles que : et .
Comme , la parabole est tournée vers le bas c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
On en déduit le tableau de signe de ainsi que le tableau de variation de . On indiquera les valeurs des extrema.
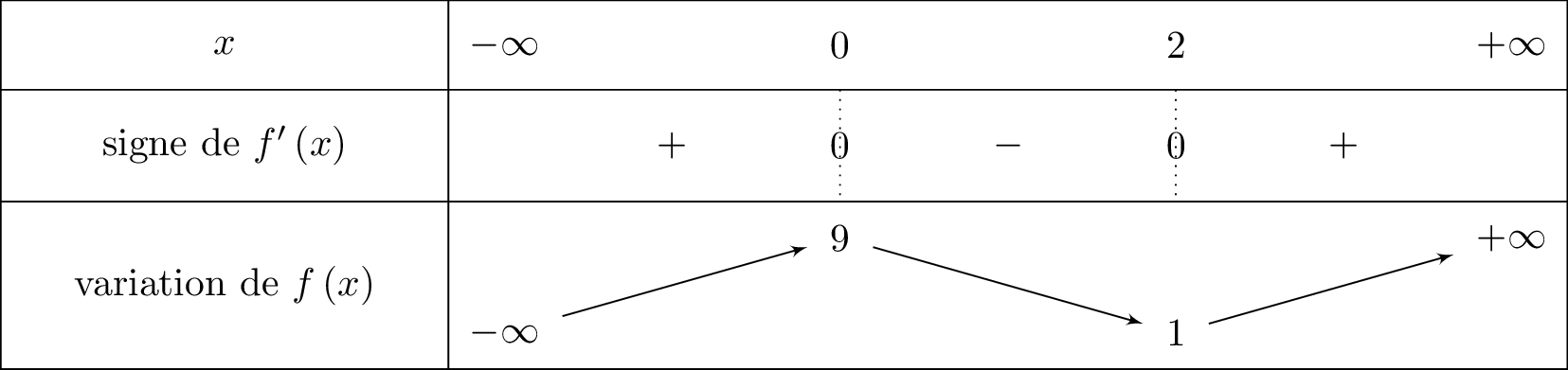 donc
donc
donc
. Il s'agit d'une équation du second degré, on calcule le discriminant et on détermine les racines.
Ainsi : , il existe donc deux racines réelles distinctes telles que : et .
Comme , la parabole est tournée vers le bas c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
On en déduit le tableau de signe de ainsi que le tableau de variation de . On indiquera les valeurs des extrema.

donc
Question 3
Démontrer que l'équation admet une unique solution sur .
On notera cette solution.
On notera cette solution.
Correction
On reprend le tableau de variation fait à la question . On fera apparaître le zéro que l'on recherche. 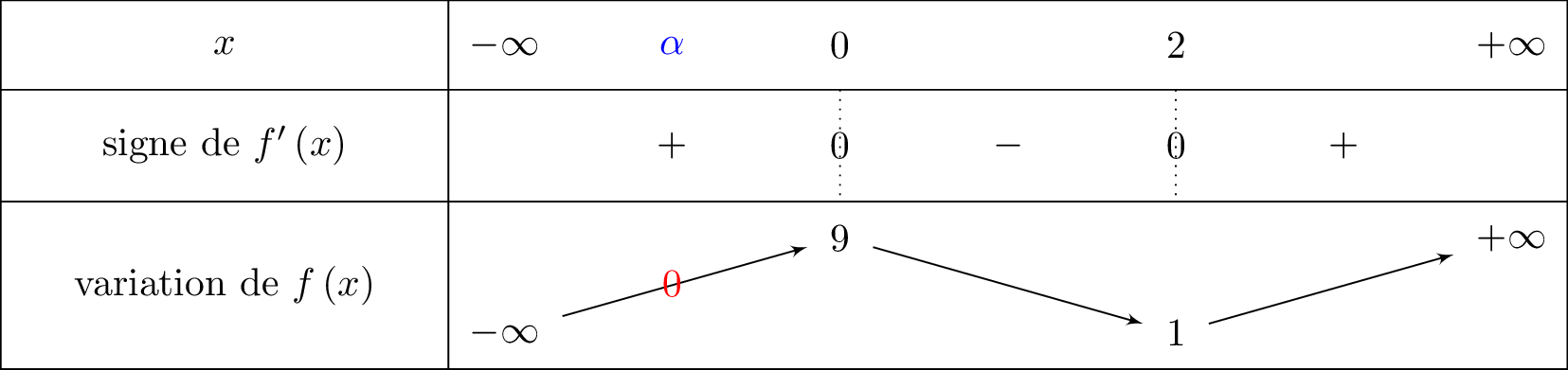 De plus :
De plus :
et
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :

- Sur , la fonction est continue et admet comme minimum.
La fonction est strictement positive.
Donc l'équation n'a pas de solution sur cet intervalle. - Sur , la fonction est continue et strictement croissante.
De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que
et
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
Question 4
En déduire le signe de sur l'intervalle .
Correction

Sur , la fonction est continue et strictement croissante et
Donc pour tout et pour tout
On résume cela dans un tableau de signe :
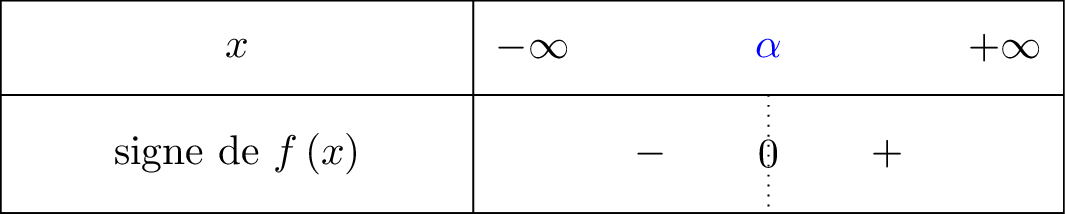
Question 5
Déterminer une équation de la tangente à la courbe au point d'abscisse .
Correction
L'équation de la tangente au point d'abscisse s'écrit .
Ici , ce qui donne : 1ère étape : calculer
2ème étape : calculer
3ème étape : on remplace les valeurs de et de dans la formule de l'équation de tangente.
On sait que :
Ainsi l'équation de la tangente à la courbe au point d'abscisse est alors .