Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ère partie - Exercice 2
50 min
75
Soit la fonction définie sur par .
Question 1
Déterminer la limite de la fonction en et en
Correction
D'une part : . Au voisinage de , un polynôme est équivalent à son monôme de plus haut degré. Autrement dit, on n'étudie que la limite du monôme de plus haut degré.
Donc :
D'autre part : . Au voisinage de , un polynôme est équivalent à son monôme de plus haut degré. Autrement dit, on n'étudie que la limite du monôme de plus haut degré.
Donc :
Donc :
D'autre part : . Au voisinage de , un polynôme est équivalent à son monôme de plus haut degré. Autrement dit, on n'étudie que la limite du monôme de plus haut degré.
Donc :
Question 2
Déterminer le tableau de variation de la fonction sur
Correction
est dérivable sur .
On va commencer par calculer la dérivée de .
Il vient alors que :
est dérivable sur , pour tout réel , on a :
, c'est une équation du second degré, on calcule le discriminant et on détermine les racines.
Ainsi : , il existe donc deux racines réelles distinctes telles que : et .
Comme , la parabole est tournée vers le haut c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
On en déduit le tableau de signe de ainsi que le tableau de variation de . On indiquera les valeurs des extrema.
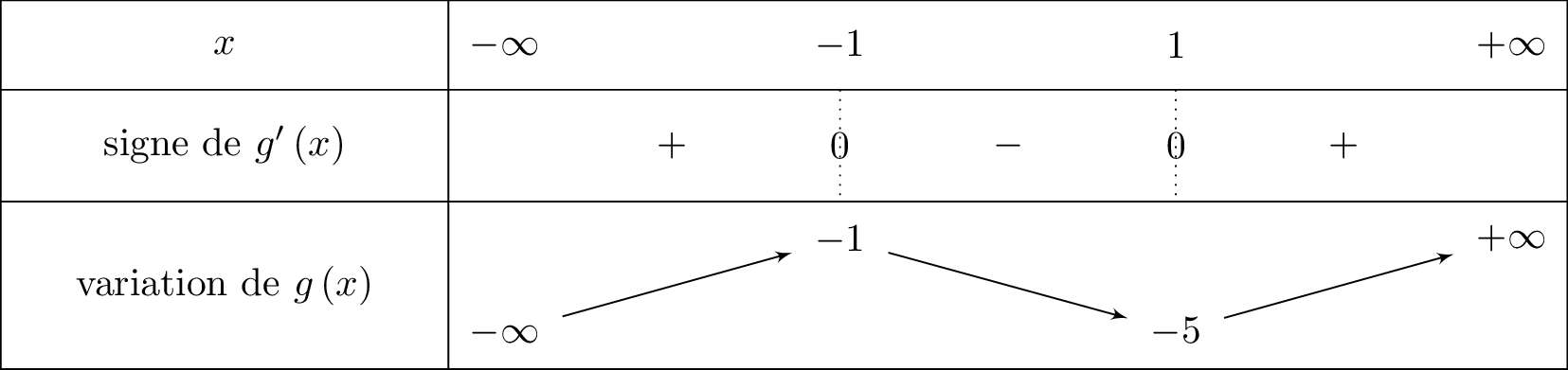 De plus:
De plus:
ainsi
ainsi
On va commencer par calculer la dérivée de .
Il vient alors que :
est dérivable sur , pour tout réel , on a :
, c'est une équation du second degré, on calcule le discriminant et on détermine les racines.
Ainsi : , il existe donc deux racines réelles distinctes telles que : et .
Comme , la parabole est tournée vers le haut c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
On en déduit le tableau de signe de ainsi que le tableau de variation de . On indiquera les valeurs des extrema.

ainsi
ainsi
Question 3
Démontrer que l'équation admet une unique solution sur
On notera cette solution.
On notera cette solution.
Correction
On reprend le tableau de variation fait à la question .
On fera apparaître le zéro que l'on recherche.
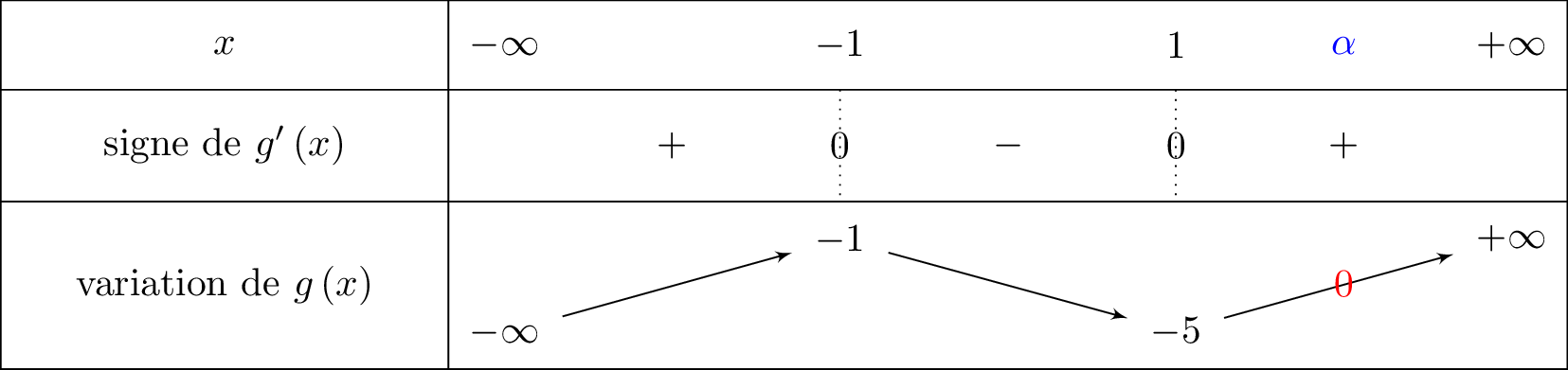 De plus :
De plus :
On fera apparaître le zéro que l'on recherche.

- Sur , la fonction est continue et admet comme maximum.
La fonction est strictement négative.
Donc l'équation n'a pas de solution sur cet intervalle. - Sur , la fonction est continue et strictement croissante.
De plus, et
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que
Question 4
Déterminer un encadrement de à près.
Correction
A la calculatrice, on vérifie que :
et
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
et
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
Question 5
Déterminer le signe de la fonction sur
Correction

Sur , la fonction est continue et strictement croissante et
Donc pour tout et pour tout
On résume cela dans un tableau de signe :

Question 6
On considère la fonction définie par :
Déterminer le domaine de définition de
Correction
est une fraction rationnelle.
est définie pour toutes les valeurs réelles sauf celles qui annulent le dénominateur.
Résolvons donc .
Il s'agit d'une équation du second degré, on utilise donc le discriminant.
On donnera directement les résultats : équivaut à :
Il en résulte que le domaine de définition est :
ou encore
est définie pour toutes les valeurs réelles sauf celles qui annulent le dénominateur.
Résolvons donc .
Il s'agit d'une équation du second degré, on utilise donc le discriminant.
On donnera directement les résultats : équivaut à :
Il en résulte que le domaine de définition est :
ou encore
Question 7
Déterminer ensuite les limites de aux bornes de son domaine de définition.
Que peut-on en déduire graphiquement ?
Que peut-on en déduire graphiquement ?
Correction
On va calculer la limite en par les deux méthodes proposées en terminale S :
Méthode 1 :
(au voisinage de , on ne garde que les monômes de plus haut degré au numérateur et au dénominateur)
Ainsi :
Finalement :
Méthode 2 : Au voisinage de , on factorise par le monôme de plus haut degré.
(au voisinage de , on factorise par le monôme du plus haut degré au numérateur et on factorise par le monôme du plus haut degré au dénominateur)
Ainsi :
D'où : par quotient :
Finalement :
On va calculer la limite en par les deux méthodes proposées en terminale S :
Méthode 1 :
(au voisinage de , on ne garde que les monômes de plus haut degré au numérateur et au dénominateur)
Ainsi :
Finalement :
Méthode 2 : Au voisinage de , on factorise par le monôme de plus haut degré.
(au voisinage de , on ne garde que les monômes de plus haut degré au numérateur et au dénominateur)
Ainsi :
D'où : par quotient :
Finalement :
On va calculer la limite en :
Il en résulte que la droite d'équation
On va calculer la limite en :
Il en résulte que la droite d'équation
On va calculer la limite en :
Il en résulte que la droite d'équation
On va calculer la limite en :
Il en résulte que la droite d'équation
Méthode 1 :
(au voisinage de , on ne garde que les monômes de plus haut degré au numérateur et au dénominateur)
Ainsi :
Finalement :
Méthode 2 : Au voisinage de , on factorise par le monôme de plus haut degré.
(au voisinage de , on factorise par le monôme du plus haut degré au numérateur et on factorise par le monôme du plus haut degré au dénominateur)
Ainsi :
D'où : par quotient :
Finalement :
On va calculer la limite en par les deux méthodes proposées en terminale S :
Méthode 1 :
(au voisinage de , on ne garde que les monômes de plus haut degré au numérateur et au dénominateur)
Ainsi :
Finalement :
Méthode 2 : Au voisinage de , on factorise par le monôme de plus haut degré.
(au voisinage de , on ne garde que les monômes de plus haut degré au numérateur et au dénominateur)
Ainsi :
D'où : par quotient :
Finalement :
On va calculer la limite en :
Il en résulte que la droite d'équation
est asymptote verticale à la courbe représentative de la fonction .
On va calculer la limite en :
Il en résulte que la droite d'équation
est asymptote verticale à la courbe représentative de la fonction .
On va calculer la limite en :
Il en résulte que la droite d'équation
est asymptote verticale à la courbe représentative de la fonction .
On va calculer la limite en :
Il en résulte que la droite d'équation
est asymptote verticale à la courbe représentative de la fonction .
Question 8
On rappelle que :
Démontrer que pour tout réel du domaine de définition de , on a :
Correction
est dérivable sur
On reconnait la forme avec et
Ainsi : et
Il vient alors que :
équivaut successivement à :
. Nous allons factoriser par . Ce qui nous donne :
On reconnait la forme avec et
Ainsi : et
Il vient alors que :
équivaut successivement à :
. Nous allons factoriser par . Ce qui nous donne :
Question 9
En déduire les variations de la fonction
Correction
Rappelons que et sont les valeurs interdites.
On en déduit le tableau de variation de :
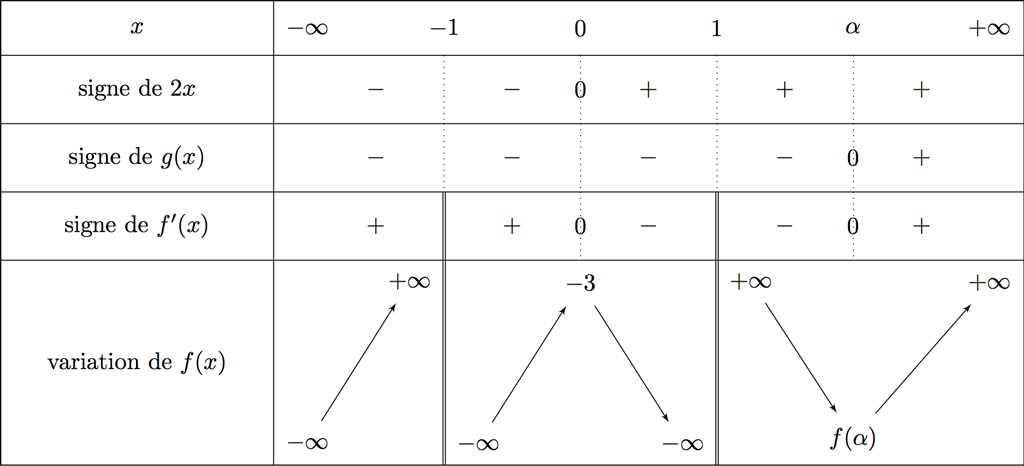
On en déduit le tableau de variation de :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.