Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Résoudre les inéquations - Exercice 1
12 min
30
Résoudre dans les inéquations suivantes :
Question 1
Correction
Le domaine de définition impose que et l'inéquation est vraie si .
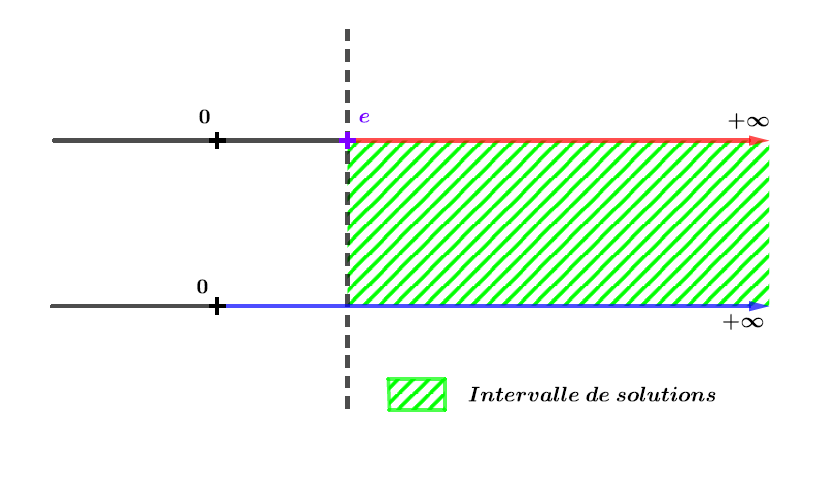
On garde la zone où les deux ensembles sont coloriés simultanément.
Ici c'est la zone à droite de la barre pointillée verticale.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
Question 2
Correction
Le domaine de définition impose que et l'inéquation est vraie si .
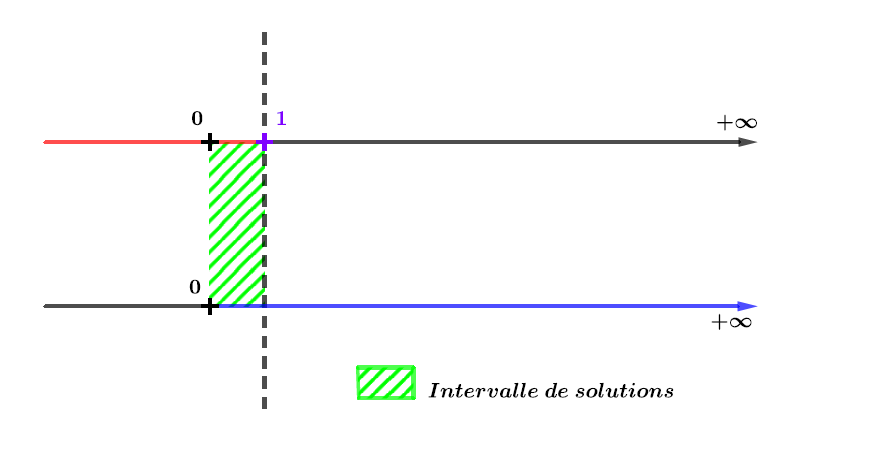
On garde la zone où les deux ensembles sont coloriés simultanément.
Ici c'est la zone à gauche de la barre pointillée verticale.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
Question 3
Correction
équivaut successivement à
Le domaine de définition impose que et l'inéquation est vraie si .
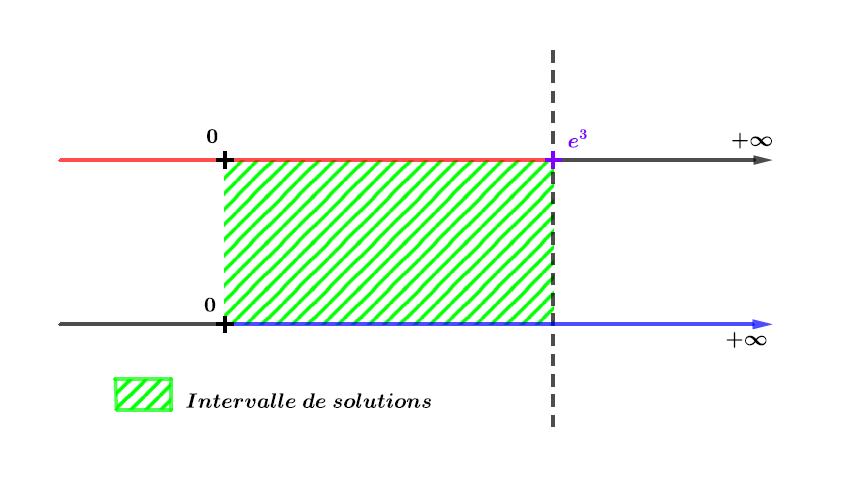
On garde la zone où les deux ensembles sont coloriés simultanément.
Ici c'est la zone à gauche de la barre pointillée verticale.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
Question 4
Correction
équivaut successivement à
Le domaine de définition impose que et l'inéquation est vraie si .
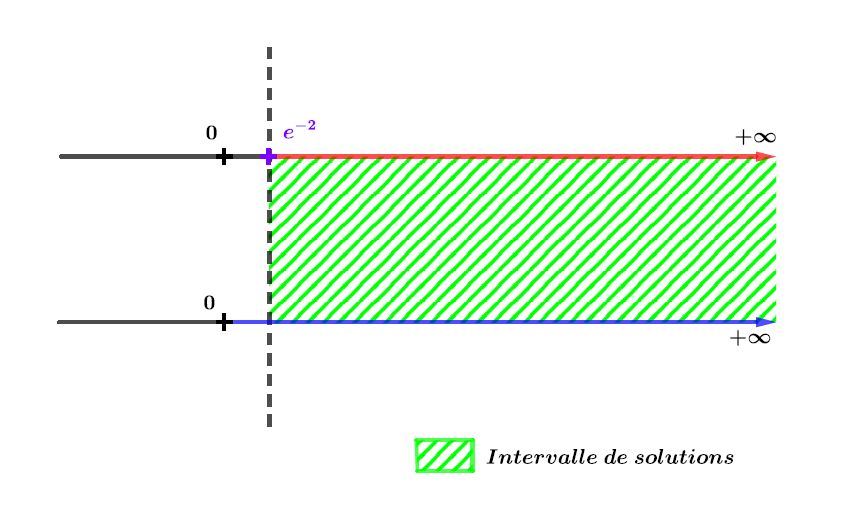
On garde la zone où les deux ensembles sont coloriés simultanément.
Ici c'est la zone à droite de la barre pointillée verticale.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
Question 5
Correction
équivaut successivement à
Le domaine de définition impose que et l'inéquation est vraie si .
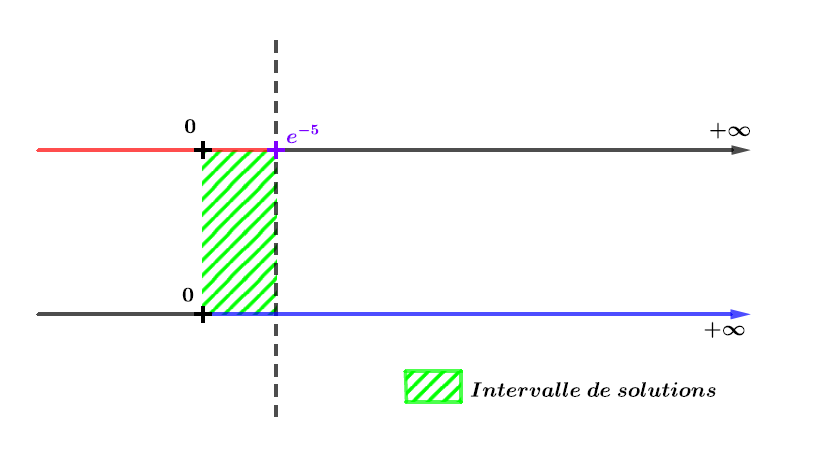
On garde la zone où les deux ensembles sont coloriés simultanément.
Ici c'est la zone à gauche de la barre pointillée verticale.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.