Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Les limites avec la fonction - Exercice 1
15 min
30
Question 1
Déterminer les limites suivantes :
Correction
Ici, il s'agit d'une limite par composition.
On commence par calculer .
On pose .
Ainsi : .
Par composition :
On commence par calculer .
On pose .
Ainsi : .
Par composition :
Question 2
Correction
Ici, il s'agit d'une limite par composition.
On commence par calculer .
On pose .
Ainsi : .
Par composition :
On commence par calculer .
On pose .
Ainsi : .
Par composition :
Question 3
Correction
Ici, il s'agit d'une limite par composition.
On commence par calculer .
On pose .
Ainsi : .
Par composition :
On commence par calculer .
On pose .
Ainsi : .
Par composition :
Question 4
Correction
Ici, il s'agit d'une limite par composition.
On commence par calculer . Le tableau de signe ci-dessous nous explique pourquoi
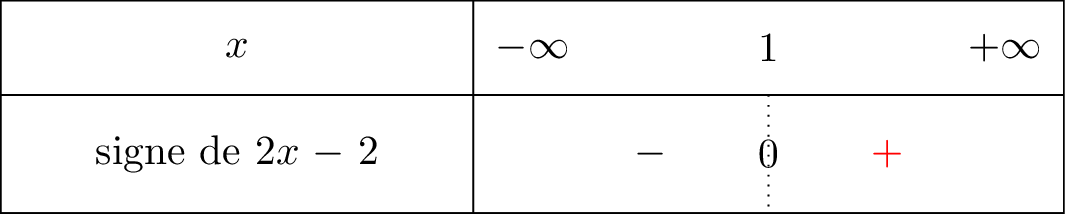 On pose .
On pose .
Ainsi : .
Par composition :
On commence par calculer . Le tableau de signe ci-dessous nous explique pourquoi

Ainsi : .
Par composition :
Question 5
Correction
Ici, il s'agit d'une limite par composition.
On pose .
Ainsi : .
Par composition :