Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Etude de fonctions - Exercice 1
35 min
45
Etudiez les variations des fonctions suivantes sur
Question 1
Correction
est dérivable sur .
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
On en déduit le tableau de variation suivant :
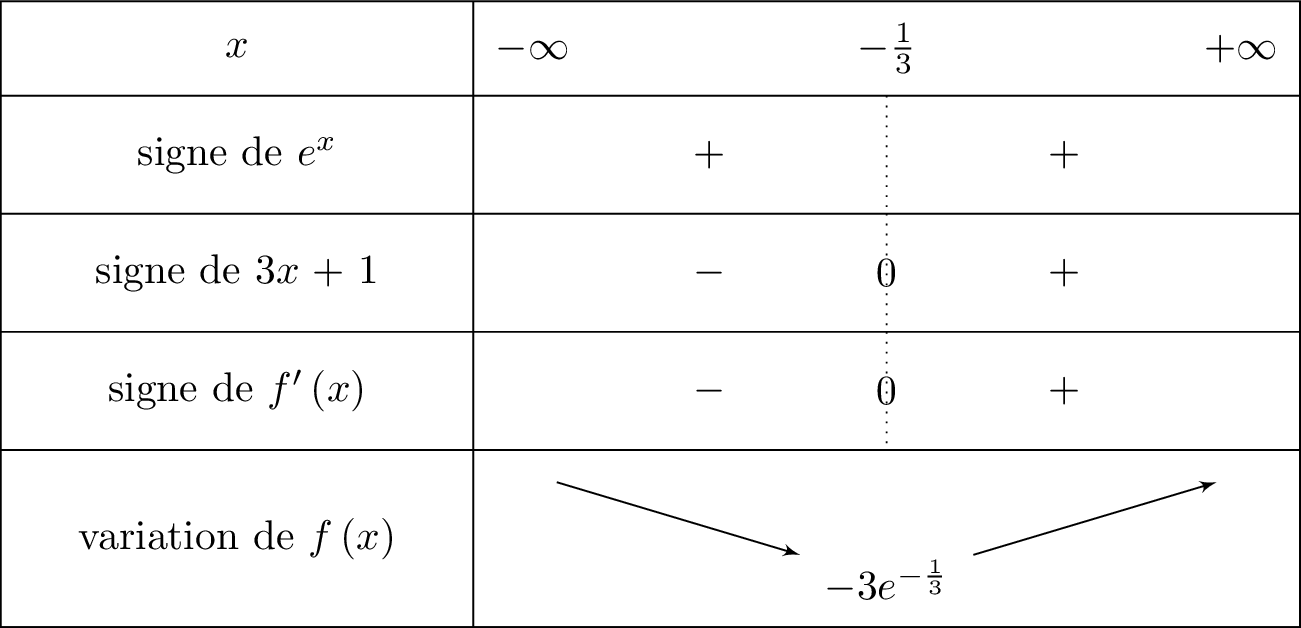
De plus :
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Il faut penser à factoriser par les exponentielles afin de faciliter les études de signes.
Pour tout réel , on a .Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
On en déduit le tableau de variation suivant :

De plus :
Question 2
Correction
est dérivable sur .
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
On en déduit le tableau de variation suivant :
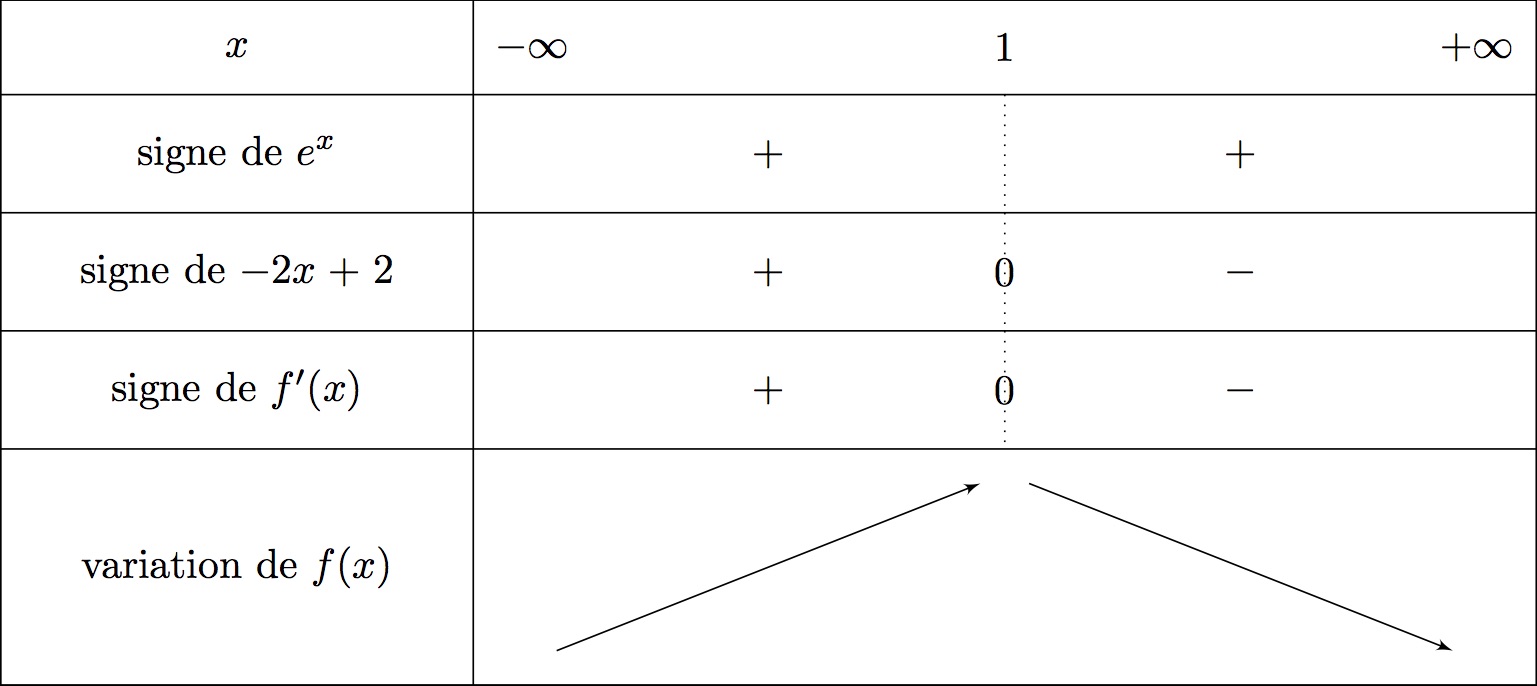
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Il faut penser à factoriser par les exponentielles afin de faciliter les études de signes.
Pour tout réel , on a .On en déduit le tableau de variation suivant :

Question 3
Correction
est dérivable sur .
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que
Pour l'étude de , on va utiliser le discriminant.
Nous donnons directement les résultats car le discriminant n'a maintenant plus de secret pour nous. , et .
On en déduit le tableau de variation suivant :
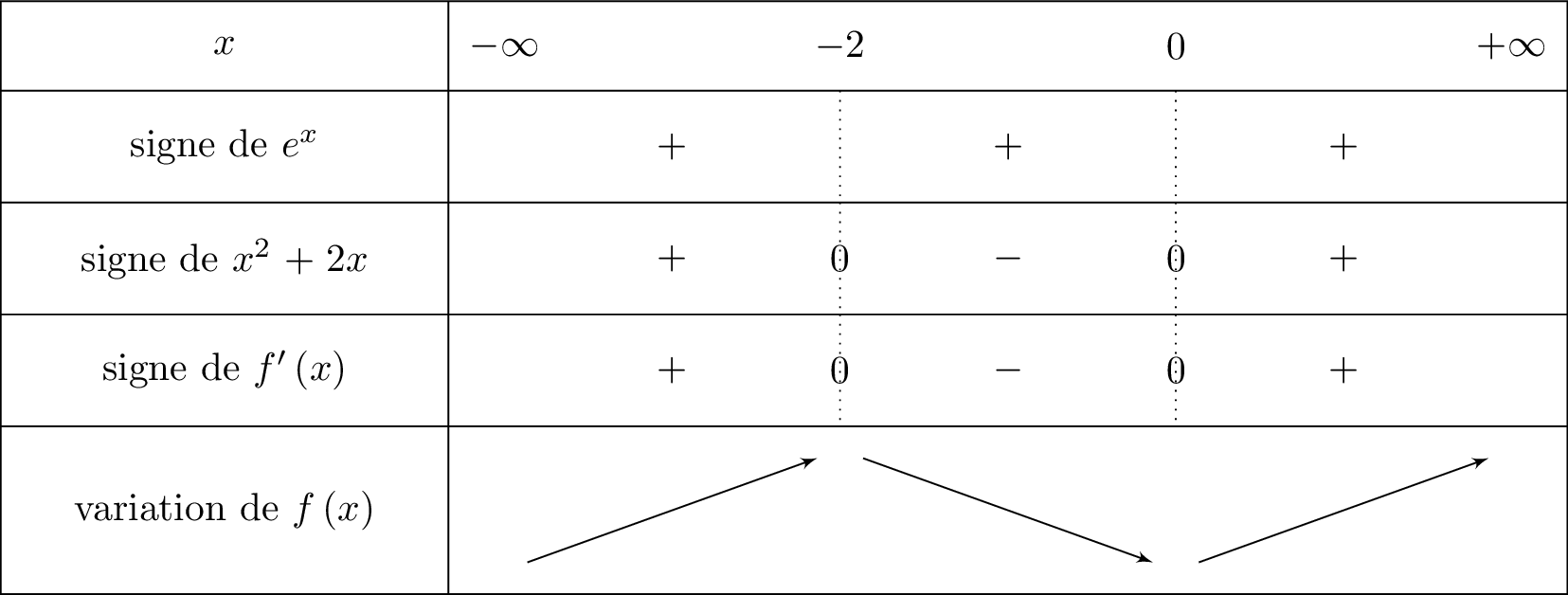
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que
Il faut penser à factoriser par les exponentielles afin de faciliter les études de signes.
Pour tout réel , on a .Pour l'étude de , on va utiliser le discriminant.
Nous donnons directement les résultats car le discriminant n'a maintenant plus de secret pour nous. , et .
On en déduit le tableau de variation suivant :

Question 4
Correction
est dérivable sur .
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Pour l'étude de , on va utiliser le discriminant.
Nous donnons directement les résultats car le discriminant n'a maintenant plus de secret pour nous. , et .
On en déduit le tableau de variation suivant :
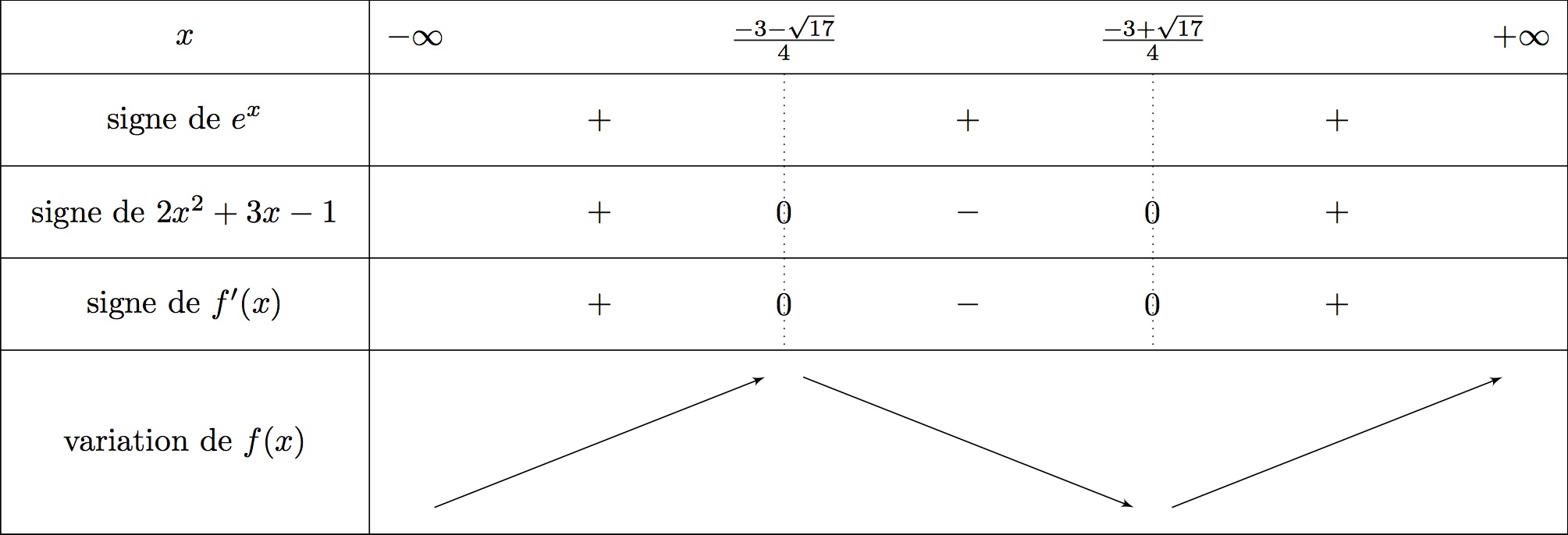
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Il faut penser à factoriser par les exponentielles afin de faciliter les études de signes.
Pour tout réel , on a .Pour l'étude de , on va utiliser le discriminant.
Nous donnons directement les résultats car le discriminant n'a maintenant plus de secret pour nous. , et .
On en déduit le tableau de variation suivant :

Question 5
Correction
Ici on reconnait la forme : avec et .
Ainsi : et .
Il vient alors que :
équivaut successivement à :
Pour tout réel , on a , il vient alors que
Pour tout réel , on a .
On en déduit le tableau de variation suivant :

Ainsi : et .
Il vient alors que :
équivaut successivement à :
Pour tout réel , on a , il vient alors que
Pour tout réel , on a .
On en déduit le tableau de variation suivant :

Question 6
Correction
est dérivable sur .
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
On en déduit le tableau de variation suivant :
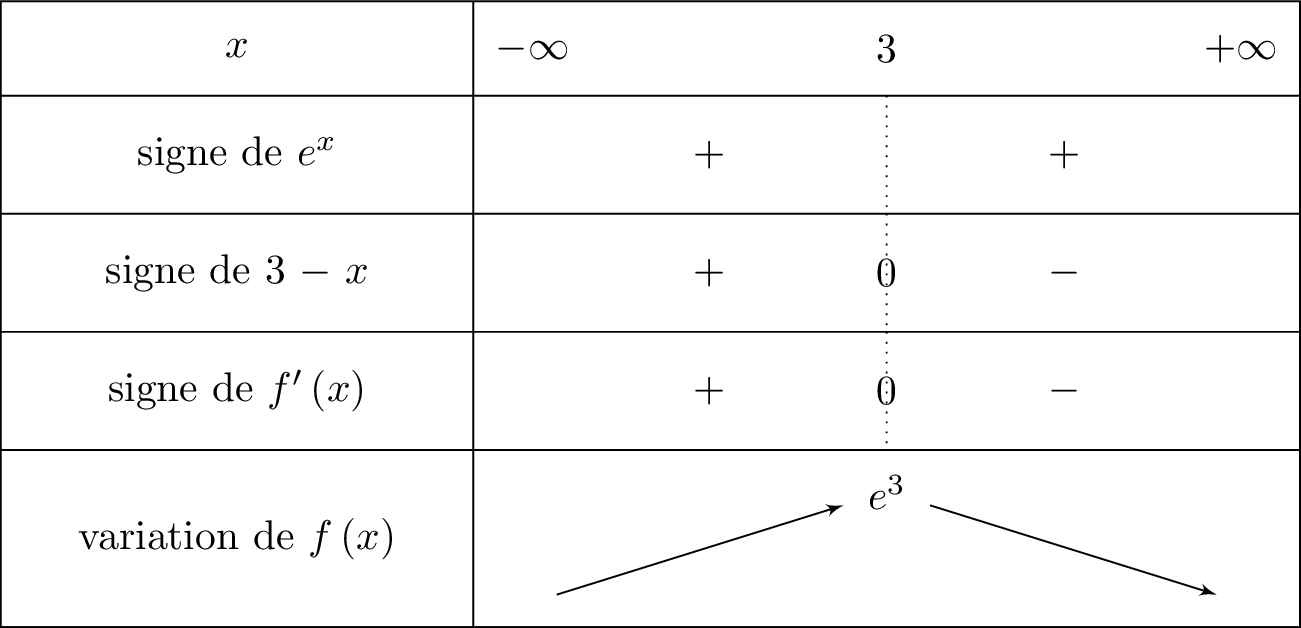
De plus :
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Il faut penser à factoriser par les exponentielles afin de faciliter les études de signes.
Pour tout réel , on a .Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
On en déduit le tableau de variation suivant :

De plus :
Question 7
Correction
est dérivable sur .
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Pour tout réel , on a et . Il en résulte donc que : et de ce fait .
On en déduit le tableau de variation suivant :
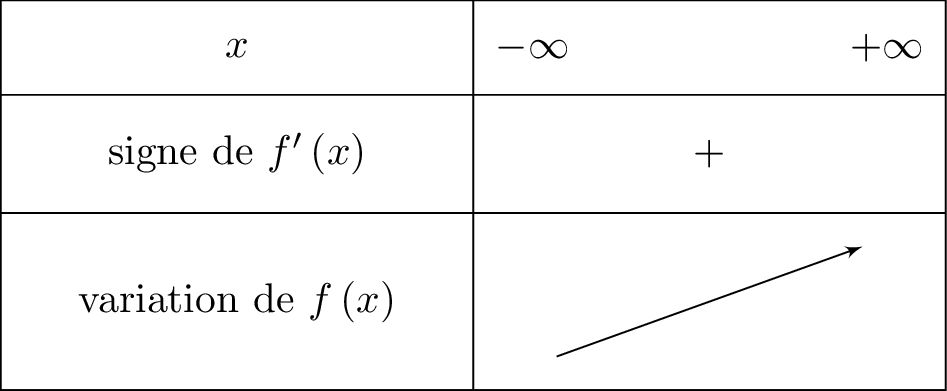
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Pour tout réel , on a et . Il en résulte donc que : et de ce fait .
On en déduit le tableau de variation suivant :
