Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Convexité et lecture graphique - Exercice 1
10 min
15
On considère une fonction définie sur et deux fois dérivable.
On donne ci-dessous la courbe représentative de la fonction , dérivée seconde de la fonction , dans un repère orthonormé.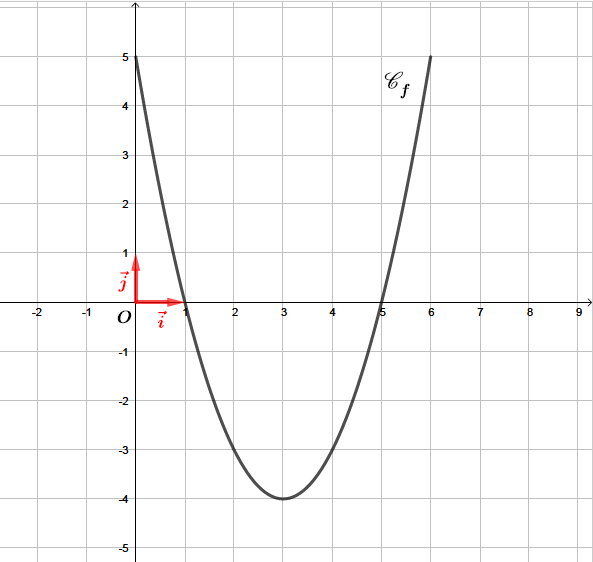
On donne ci-dessous la courbe représentative de la fonction , dérivée seconde de la fonction , dans un repère orthonormé.

Question 1
La courbe représentative de admet-elle des points d'inflexion ?
Correction
- possède un point d'inflexion lorsque sa dérivée seconde s'annule et change de signe en ce point.
Les solutions de sont donc et . Il s'agit des points d'intersections entre la courbe et l'axe des abscisses.
La courbe admet donc deux points d'inflexions aux points d'abscisses et .
Question 2
Sur quels intervalles, la fonction est-elle convexe ? Est-elle concave ?
Correction
Pour étudier la convexité de la fonction , il faut étudier le signe de .
D'après le graphique, on voit que :
sur un intervalle
sur un intervalle
On résume cela dans un tableau :
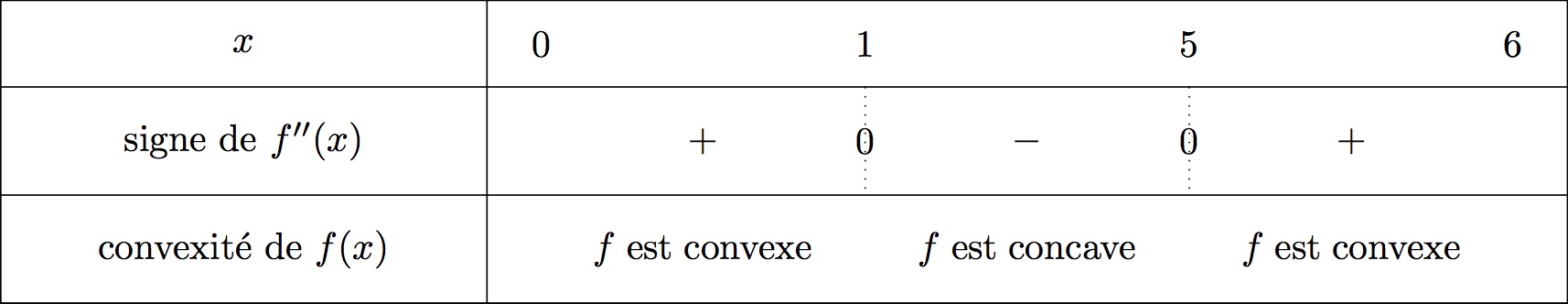
- Lorsque sur un intervalle alors est convexe.
- Lorsque sur un intervalle alors est concave.
sur un intervalle
sur un intervalle
On résume cela dans un tableau :
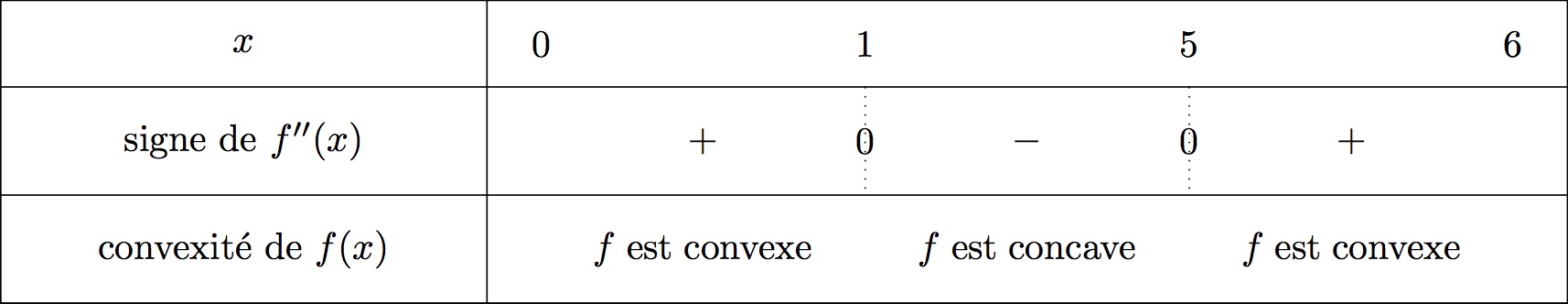
Question 3
On donne la dérivée de la fonction .
Donner le tableau de variation de la fonction .
Donner le tableau de variation de la fonction .
Correction
- Lorsque sur un intervalle alors est croissante sur.
- Lorsque sur un intervalle alors est décroissante sur.
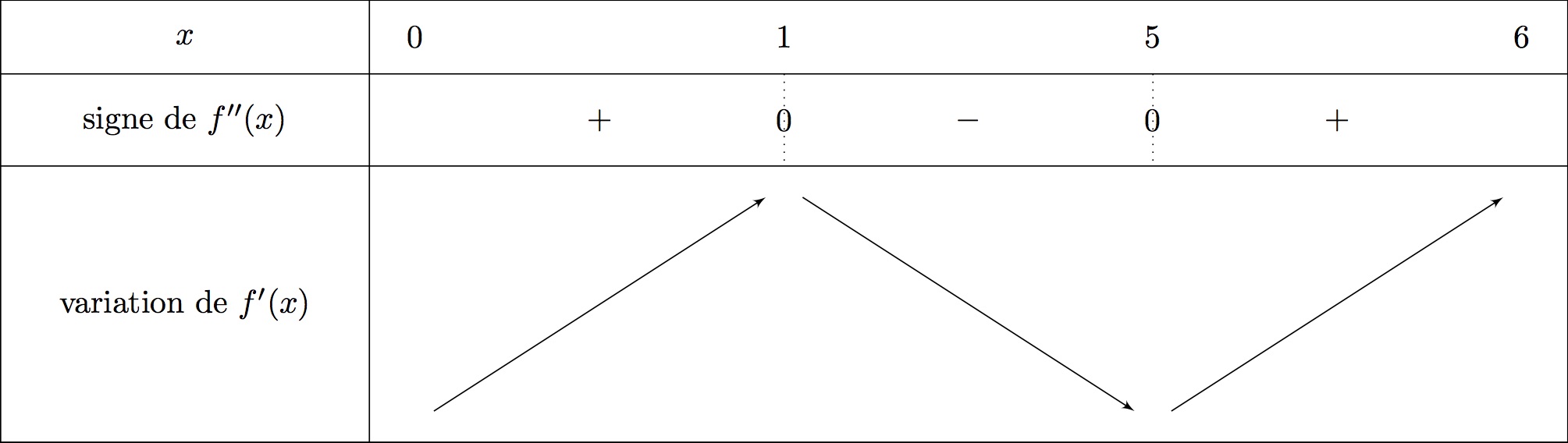
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.