Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Loi binomiale - Exercice 3
30 min
45
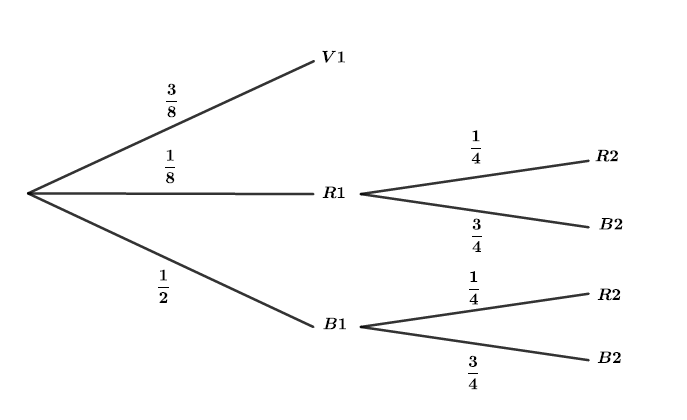
Dans une fête foraine, un organisateur de jeux dispose de urnes comportant chacune boules.
L'urne comporte boules vertes, boule rouge et boules bleues.
L'urne comporte boules bleues et boules rouges.
Le déroulement du jeu est le suivant :
Le joueur tire une boule de l'urne :
L'urne comporte boules vertes, boule rouge et boules bleues.
L'urne comporte boules bleues et boules rouges.
Le déroulement du jeu est le suivant :
Le joueur tire une boule de l'urne :
- S'il tombe sur une boule verte le jeu s'arrête.
- S'il tombe sur une boule rouge ou bleue, il tire une boule de l'urne .
- V1 l'événement : "la boule est verte lors du premier tirage dans l'urne".
- R1 l'événement : "la boule est rouge lors du premier tirage dans l'urne".
- B1 l'événement : "la boule est bleue lors du premier tirage dans l'urne".
- R2 l'événement : "la boule est rouge lors du deuxième tirage dans l'urne".
- B2 l'événement : "la boule est bleue lors du deuxième tirage dans l'urne".
Question 1
Construire un arbre pondéré résumant la situation.
Correction
On remplit l'arbre pondéré avec les données de l'exercice.

Question 2
Calculer la probabilité de l'évènement "tirer deux boules bleues"
Correction

D'après la formule des probabilités totales on a :
Calculons
d'où
On a trois chances sur de tirer deux boules bleues.
Question 3
Calculer la probabilité de l'évènement "tirer une boule rouge"
Correction

- soit en er on tire une rouge puis ensuite une bleue.
- soit en er on tire une bleue puis ensuite une rouge.
Ainsi,
équivaut successivement à
On a chances sur de tirer une boule rouge.
Question 4
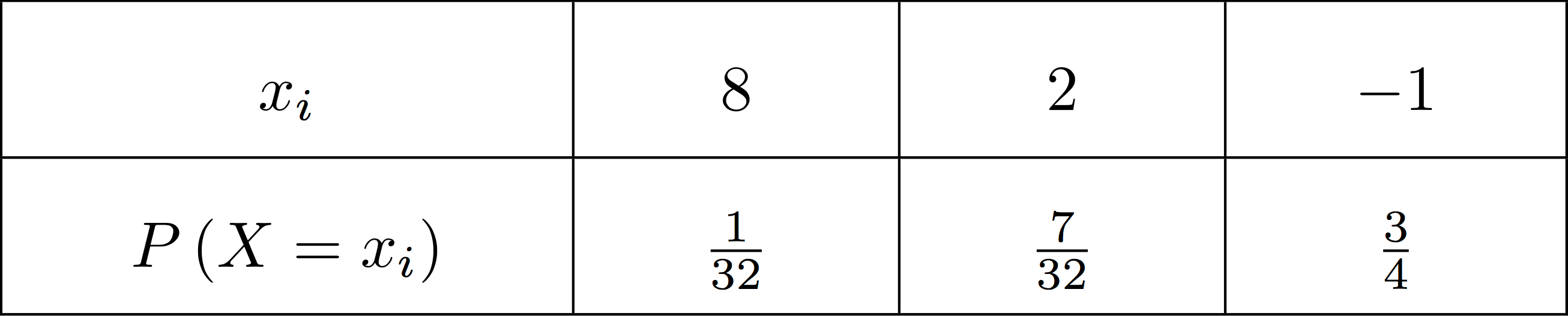
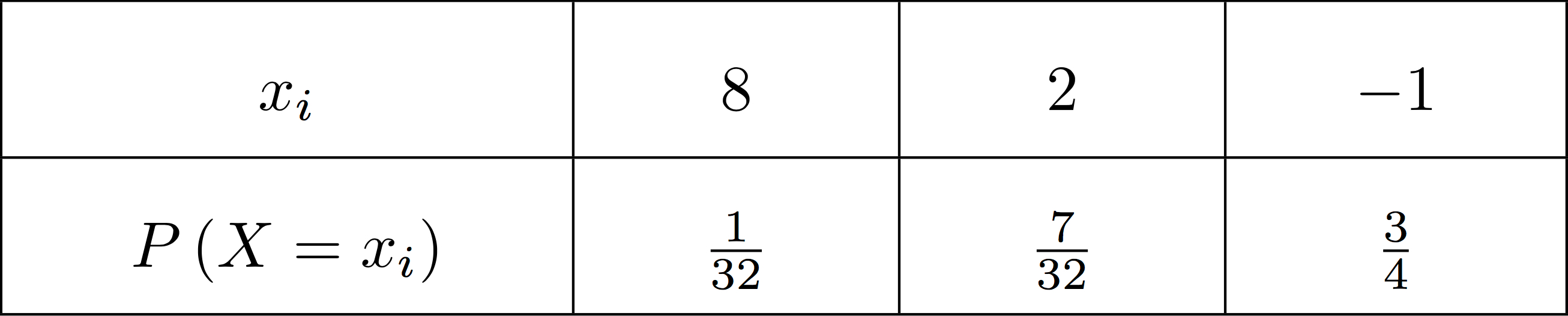
Si les deux boules sont rouges, le joueur gagne €, si une boule est rouge, il gagne €, sinon il ne gagne rien.
Le joueur mise €. Soit la variable aléatoire représentant le gain du joueur.
Déterminer la loi de probabilité de .
Le joueur mise €. Soit la variable aléatoire représentant le gain du joueur.
Déterminer la loi de probabilité de .
Correction

Nous avons déjà calculé à la question .
Calculons,
équivaut successivement à
Le gain du joueur est la somme reçue moins sa mise.
Ainsi, prendra les valeurs
On va traduire ces informations dans un tableau que l'on appellera loi de probabilité :
Soit
Ainsi :
Question 5
Calculer l'espérance mathématiques de et en donner une interprétation.
Correction
On appelle l'espérance mathématique de la variable , la valeur définie par :
Autrement dit
Soit : c'est-à-dire :
En moyenne le joueur perdra € par partie en jouant un très grand nombre de fois.
Question 6
Le joueur décide de faire parties consécutives supposées indépendantes .
Justifier que la probabilité qu'il tire au moins une fois une boule de la deuxième urne est
Correction
On considère l'expérience ci-dessous
On appelle « tirer une boule dans la deuxième urne » avec la probabilité On appelle « ne pas tirer une boule dans la deuxième urne » avec la probabilité On répète fois de suite cette expérience de Bernoulli de .
On est donc en présence
est la variable aléatoire qui associe le nombre de fois que l'on tire une boule de la deuxième urne.
suit la loi binomiale de paramètre et .
On note alors suit la loi binomiale
On est donc en présence
est la variable aléatoire qui associe le nombre de fois que l'on tire une boule de la deuxième urne.
suit la loi binomiale de paramètre et .
On note alors suit la loi binomiale
Il vient alors que :
, on va utiliser l'évènement contraire, ce qui donne :
On rappelle que et
Question 7
Déterminer la limite de la suite
Correction
- Si alors .
- Si alors .
On sait que donc
Il en résulte que :
Question 8
A l'aide de la calculatrice, déterminer la plus petite valeur de telle que .
Correction
A l'aide de la calculatrice, à partir de , on a
Il est aussi possible de répondre à cette question en utilisant le logarithme (à ne prendre en compte que si tu l'as vu avec ton enseignant, mais au bac, cette question est souvent demandé).
équivaut successivement à
car
, on a changé le sens de l'inéquation car
On cherche la valeur de à la calculatrice et on arrondi à l'entier supérieur.
Il est aussi possible de répondre à cette question en utilisant le logarithme (à ne prendre en compte que si tu l'as vu avec ton enseignant, mais au bac, cette question est souvent demandé).
équivaut successivement à
car
, on a changé le sens de l'inéquation car
On cherche la valeur de à la calculatrice et on arrondi à l'entier supérieur.
(à la calculatrice on obtient et on arrondi à l'entier supérieur).
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.