Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Diagramme en barre associé à une loi binomiale - Exercice 2

3 min
10
Soit XX une variable aléatoire suivant la loi binomiale de paramètres nn et pp. On donne ci-dessous le diagramme en barres à XX .
Question 1

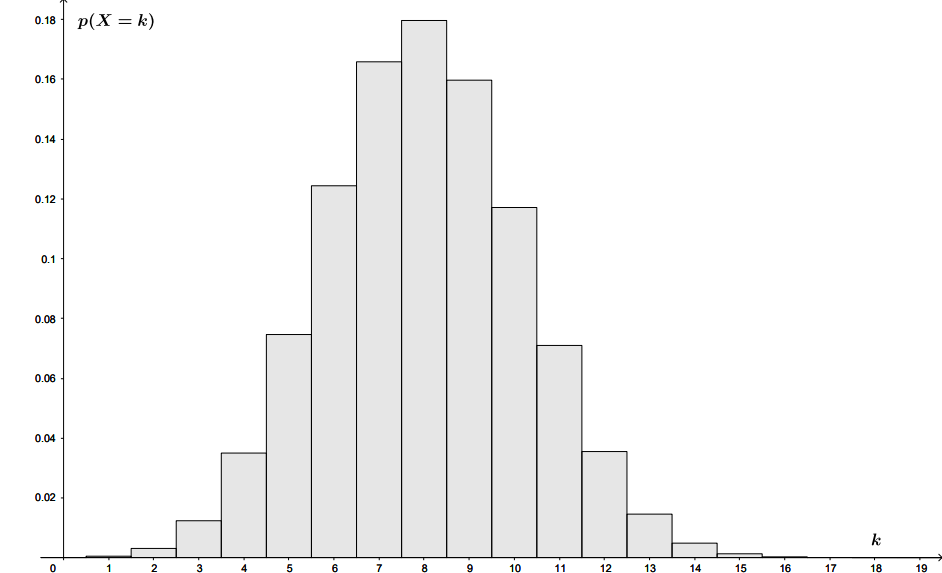
Estimer graphiquement E(X)E\left(X\right) .

Correction
    Soit XX une variable aléatoire suivant la loi binomiale B(n;p)\mathscr{B}\left(n;p\right) .
  • Le diagramme associé à XX est en forme de cloche, centreˊ\red{\text{centré}} sur son espérance E(X)E\left(X\right).
    • Le diagramme est bien en forme de cloche et le diagramme semble eˆtre centreˊ\red{\text{semble être centré}} par rapport à la droite d'équation x=8x=8 que nous avons représenté en pointillé.
    On peut alors estimer que l'espérance E(X)E\left(X\right) est égale à 88.
    Ainsi :
    E(X)=8E\left(X\right)=8
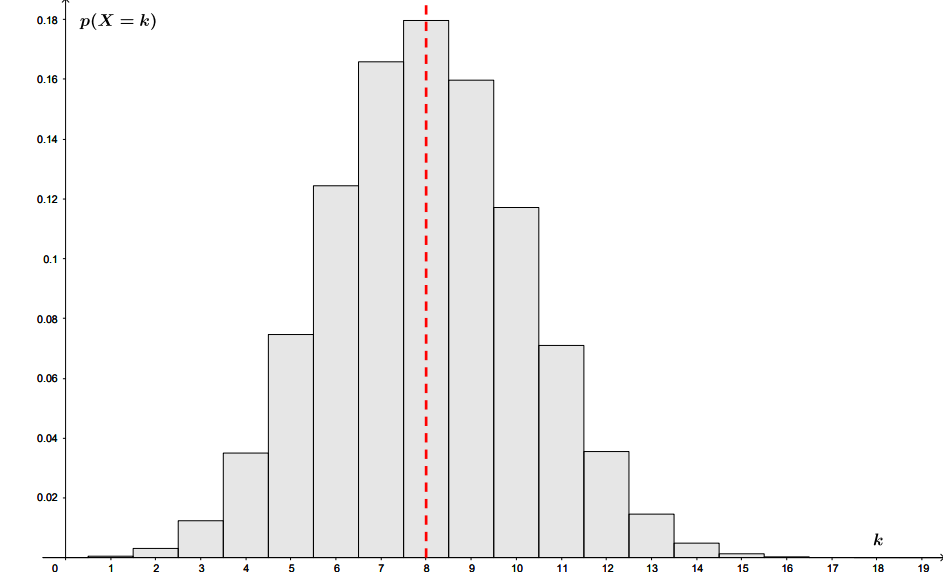
    Question 2
    On admet que n=16n=16 .

    Déterminer alors une valeur de pp .

    Correction
    XX est une variable aléatoire qui suit la loi binomiale B(n;p)\mathscr{B}\left(n;p\right) , alors l’espérance mathématique E(X)E\left(X\right) est égale à :
  • E(X)=n×pE\left(X\right)=n\times p
    • Dans notre situation, nous avons XX qui suit la loi binomiale B(16;p)\mathscr{B}\left(16;p\right) et E(X)=8E\left(X\right)=8
    Il en résulte donc que :
    16×p=816\times p=8
    p=816p=\frac{8}{16}
    Ainsi :
    p=0,5p=0,5

    On peut alors conjecturer que XX suit la loi binomiale B(16;0,5)\mathscr{B}\left(16;0,5\right) . Il s'agit d'une conjecture car notre raisonnement a été basé sur la réponse de la question 11.