Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Produit scalaire : mise en situation - Exercice 1

12 min
30
COMPETENCES‾  :  1°)  Raisonner.{\color{red}\underline{COMPETENCES}\;:\;1°)\;Raisonner.}     \;\; 2°)  Calculer.{\color{red}2°)\;Calculer.}
Soit ABCDEFGHABCDEFGH un cube d'arête 33 cm .
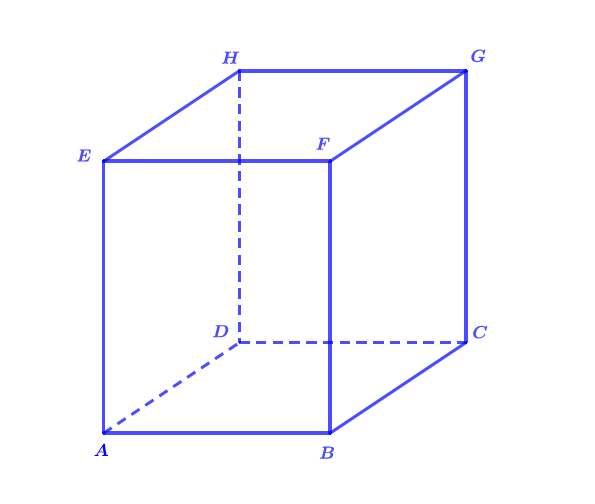
Question 1

Calculer EC→⋅AH→\overrightarrow{EC} \cdot \overrightarrow{AH}

Correction
Nous appliquons la relation de Chasles :
EC→⋅AH→=(EA→+AB→+BC→)⋅(AE→+EH→)\overrightarrow{EC} \cdot \overrightarrow{AH} =\left(\overrightarrow{E\red{A}} +\overrightarrow{\red{A}\purple{B}} +\overrightarrow{\purple{B}C} \right)\cdot \left(\overrightarrow{A\pink{E}} +\overrightarrow{\pink{E}H} \right)
EC→⋅AH→=EA→⋅AE→+EA→⋅EH→+AB→⋅AE→+AB→⋅EH→+BC→⋅AE→+BC→⋅EH→\overrightarrow{EC} \cdot \overrightarrow{AH} =\overrightarrow{EA} \cdot \overrightarrow{AE} +\overrightarrow{EA} \cdot \overrightarrow{EH} +\overrightarrow{AB} \cdot \overrightarrow{AE} +\overrightarrow{AB} \cdot \overrightarrow{EH} +\overrightarrow{BC} \cdot \overrightarrow{AE} +\overrightarrow{BC} \cdot \overrightarrow{EH}
On vérifie facilement que :
Les droites (EA)\left(EA\right) et (EH)\left(EH\right) sont orthogonales donc EA→⋅EH→=0\overrightarrow{EA} \cdot \overrightarrow{EH}=0
Les droites (AB)\left(AB\right) et (AE)\left(AE\right) sont orthogonales donc AB→⋅AE→=0\overrightarrow{AB} \cdot \overrightarrow{AE}=0
Les droites (AB)\left(AB\right) et (EH)\left(EH\right) sont orthogonales donc AB→⋅EH→=0\overrightarrow{AB} \cdot \overrightarrow{EH}=0
les droites (BC)\left(BC\right) et (AE)\left(AE\right) sont orthogonales donc BC→⋅AE→=0\overrightarrow{BC} \cdot \overrightarrow{AE}=0
Il vient alors que :
EC→⋅AH→=EA→⋅AE→+0+0+0+0+BC→⋅EH→\overrightarrow{EC} \cdot \overrightarrow{AH} =\overrightarrow{EA} \cdot \overrightarrow{AE} +0+0+0+0 +\overrightarrow{BC} \cdot \overrightarrow{EH}
  • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de même sens alors : AB→⋅AC→=AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =AB\times AC
  • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de sens opposés alors : AB→⋅AC→=−AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =-AB\times AC
Les vecteurs EA→\overrightarrow{EA} et AE→\overrightarrow{AE} sont colinéaires et de sens opposés . Ainsi : EA→⋅AE→=−EA×AE\overrightarrow{EA} \cdot \overrightarrow{AE}=-EA\times AE
Les vecteurs BC→\overrightarrow{BC} et EH→\overrightarrow{EH} sont colinéaires et de même sens. Ainsi : BC→⋅EH→=BC×EH\overrightarrow{BC} \cdot \overrightarrow{EH}=BC \times EH
On peut maintenant écrire que :
EC→⋅AH→=EA→⋅AE→+0+0+0+0+BC→⋅EH→\overrightarrow{EC} \cdot \overrightarrow{AH} =\overrightarrow{EA} \cdot \overrightarrow{AE} +0+0+0+0+\overrightarrow{BC} \cdot \overrightarrow{EH}
EC→⋅AH→=−EA×AE+0+0+0+0+BC×EH\overrightarrow{EC} \cdot \overrightarrow{AH} =-EA\times AE+0+0+0+0+BC\times EH
EC→⋅AH→=−3×3+0+0+0+0+3×3\overrightarrow{EC} \cdot \overrightarrow{AH} =-3\times 3+0+0+0+0+3\times 3
EC→⋅AH→=−9+9\overrightarrow{EC} \cdot \overrightarrow{AH} =-9+9
Finalement :
EC→⋅AH→=0\overrightarrow{EC} \cdot \overrightarrow{AH} =0

Question 2

Calculer EC→⋅AF→\overrightarrow{EC} \cdot \overrightarrow{AF}

Correction
Nous appliquons la relation de Chasles :
EC→⋅AF→=(EA→+AB→+BC→)⋅(AB→+BF→)\overrightarrow{EC} \cdot \overrightarrow{AF} =\left(\overrightarrow{E\red{A}} +\overrightarrow{\red{A}\purple{B}} +\overrightarrow{\purple{B}C} \right)\cdot \left(\overrightarrow{A\pink{B}} +\overrightarrow{\pink{B}F} \right)
EC→⋅AF→=EA→⋅AB→+EA→⋅BF→+AB→⋅AB→+AB→⋅BF→+BC→⋅AB→+BC→⋅BF→\overrightarrow{EC} \cdot \overrightarrow{AF} =\overrightarrow{EA} \cdot \overrightarrow{AB} +\overrightarrow{EA} \cdot \overrightarrow{BF} +\overrightarrow{AB} \cdot \overrightarrow{AB} +\overrightarrow{AB} \cdot \overrightarrow{BF} +\overrightarrow{BC} \cdot \overrightarrow{AB} +\overrightarrow{BC} \cdot \overrightarrow{BF}
On vérifie facilement que :
Les droites (EA)\left(EA\right) et (AB)\left(AB\right) sont orthogonales donc EA→⋅AB→=0\overrightarrow{EA} \cdot \overrightarrow{AB}=0
Les droites (AB)\left(AB\right) et (BF)\left(BF\right) sont orthogonales donc AB→⋅BF→=0\overrightarrow{AB} \cdot \overrightarrow{BF}=0
Les droites (BC)\left(BC\right) et (AB)\left(AB\right) sont orthogonales donc BC→⋅AB→=0\overrightarrow{BC} \cdot \overrightarrow{AB}=0
les droites (BC)\left(BC\right) et (BF)\left(BF\right) sont orthogonales donc BC→⋅BF→=0\overrightarrow{BC} \cdot \overrightarrow{BF}=0
Il vient alors que :
EC→⋅AF→=0+EA→⋅BF→+AB→⋅AB→+0+0+0\overrightarrow{EC} \cdot \overrightarrow{AF} =0 +\overrightarrow{EA} \cdot \overrightarrow{BF} +\overrightarrow{AB} \cdot \overrightarrow{AB} +0+0+0
  • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de même sens alors : AB→⋅AC→=AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =AB\times AC
  • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de sens opposés alors : AB→⋅AC→=−AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =-AB\times AC
Les vecteurs EA→\overrightarrow{EA} et BF→\overrightarrow{BF} sont colinéaires et de sens opposés . Ainsi : EA→⋅BF→=−EA×BF\overrightarrow{EA} \cdot \overrightarrow{BF}=-EA\times BF
Les vecteurs AB→\overrightarrow{AB} et AB→\overrightarrow{AB} sont colinéaires et de même sens. Ainsi : AB→⋅AB→=AB×AB\overrightarrow{AB} \cdot \overrightarrow{AB}=AB \times AB
On peut maintenant écrire que :
EC→⋅AF→=0−EA×BF+AB×AB+0+0+0\overrightarrow{EC} \cdot \overrightarrow{AF} =0-EA\times BF+AB\times AB+0+0+0
EC→⋅AF→=0−3×3+3×3+0+0+0\overrightarrow{EC} \cdot \overrightarrow{AF} =0-3\times 3+3\times 3+0+0+0
EC→⋅AF→=−9+9\overrightarrow{EC} \cdot \overrightarrow{AF} =-9+9
Finalement :
EC→⋅AF→=0\overrightarrow{EC} \cdot \overrightarrow{AF} =0

Question 3

Que peut-on conclure ?

Correction
Nous avons montré que EC→⋅AH→=0\overrightarrow{EC} \cdot \overrightarrow{AH} =0 et EC→⋅AF→=0\overrightarrow{EC} \cdot \overrightarrow{AF} =0
Cela signifie que la droite (EC)\left(EC\right) est orthogonale à la droite (AH)\left(AH\right) et que la droite (EC)\left(EC\right) est également orthogonale à la droite (AF)\left(AF\right) .
Or les droites (AF)\left(AF\right) et (AH)\left(AH\right) sont coplanaires car sécantes en AA. Cela signifie donc que les vecteurs AH→\overrightarrow{AH} et AF→\overrightarrow{AF} sont non colinéaires et que les droites (AF)\left(AF\right) et (AH)\left(AH\right) appartiennent au plan (AFH)\left(AFH\right).
Finalement, la droite (EC)\left(EC\right) est orthogonale à deux vecteurs non colinéaires du plan (AFH)\left(AFH\right) donc la droite (EC)\left(EC\right) est orthogonale au plan (AFH)\left(AFH\right).