Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Montrer que deux plans sont parallèles - Exercice 1

10 min
15
Question 1
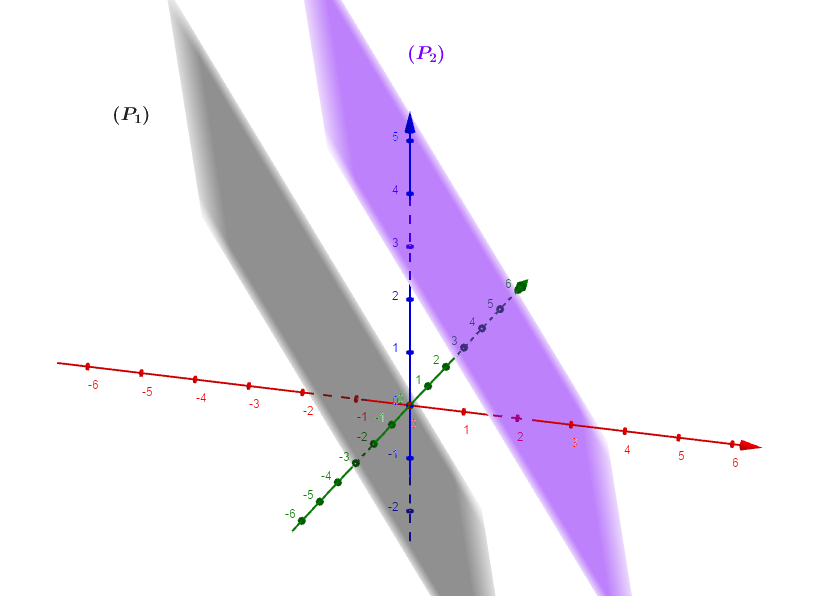
Dans l'espace muni d'un repère (O;i→;j→;k→)\left(O;\overrightarrow{i} ;\overrightarrow{j} ;\overrightarrow{k} \right), on considère les deux plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) admettant pour équation cartésienne
(P1):3x−4y+z−1=0\left(P_{1} \right):3x-4y+z-1=0 et (P2):x−y+2z+1=0\left(P_{2} \right):x-y+2z+1=0

(P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont-ils parallèles ?

Correction
    Soient n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } des vecteurs normaux respectifs des plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right).
  • si n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } sont colinéaires alors (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont parallèles.
  • si n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } ne sont pas colinéaires alors (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) ne sont pas parallèles. Cela signifie donc que les plans sont sécants.
Soient n1→(3−41)\overrightarrow{n_{1} } \left(\begin{array}{c} {3} \\ {-4} \\ {1} \end{array}\right) et n2→(1−12)\overrightarrow{n_{2} } \left(\begin{array}{c} {1} \\ {-1} \\ {2} \end{array}\right) des vecteurs normaux respectifs des plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right).
On vérifie facilement que les deux vecteurs normaux ne sont pas colinéaires (non proportionnels), alors les plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) ne sont pas parallèles.
Question 2
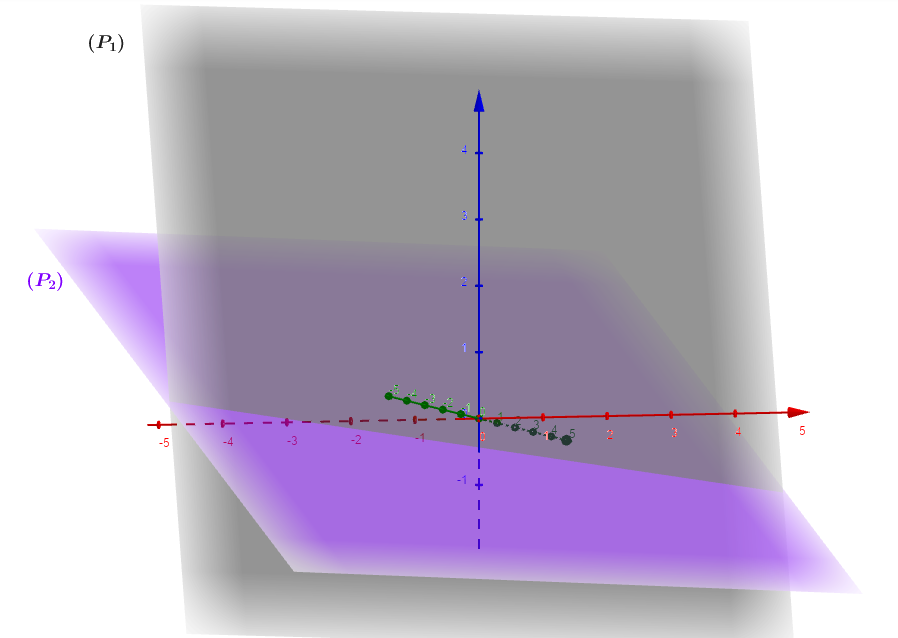
Dans l'espace muni d'un repère (O;i→;j→;k→)\left(O;\overrightarrow{i} ;\overrightarrow{j} ;\overrightarrow{k} \right), on considère les deux plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) admettant pour équation cartésienne
(P1):x−y+z−1=0\left(P_{1} \right):x-y+z-1=0 et (P2):2x−2y+2z+5=0\left(P_{2} \right):2x-2y+2z+5=0

(P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont-ils parallèles ?

Correction
    Soient n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } des vecteurs normaux respectifs des plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right).
  • si n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } sont colinéaires alors (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont parallèles.
  • si n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } ne sont pas colinéaires alors (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) ne sont pas parallèles. Cela signifie donc que les plans sont sécants.
Soient n1→(1−11)\overrightarrow{n_{1} } \left(\begin{array}{c} {1} \\ {-1} \\ {1} \end{array}\right) et n2→(2−22)\overrightarrow{n_{2} } \left(\begin{array}{c} {2} \\ {-2} \\ {2} \end{array}\right) des vecteurs normaux respectifs des plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right).
On vérifie facilement que les deux vecteurs normaux sont colinéaires car :
n2→=2×n1→\overrightarrow{n_{2} }=2\times \overrightarrow{n_{1} }
, alors les plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont parallèles.
Question 3
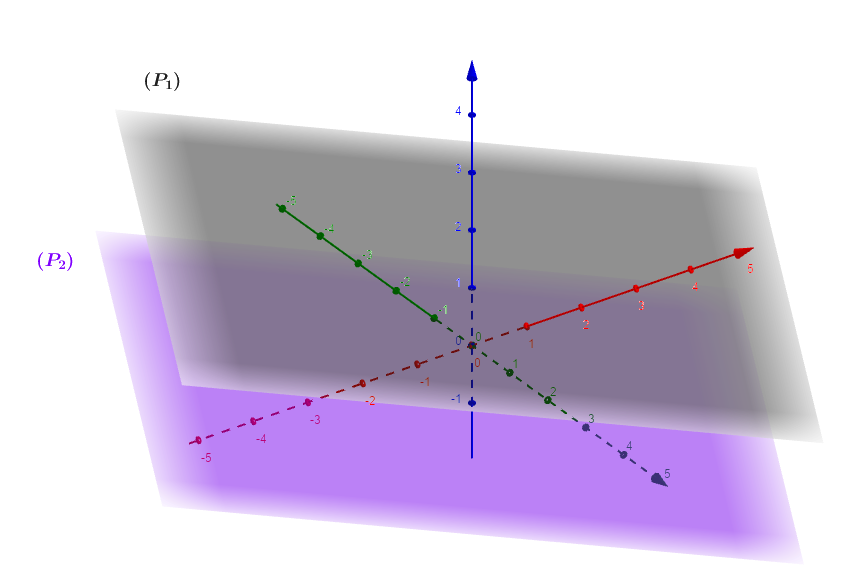
Dans l'espace muni d'un repère (O;i→;j→;k→)\left(O;\overrightarrow{i} ;\overrightarrow{j} ;\overrightarrow{k} \right), on considère les deux plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) admettant pour équation cartésienne
(P1):2x+y+4z+3=0\left(P_{1} \right):2x+y+4z+3=0 et (P2):4x+2y+8=0\left(P_{2} \right):4x+2y+8=0 .

(P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont-ils parallèles ?

Correction
    Soient n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } des vecteurs normaux respectifs des plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right).
  • si n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } sont colinéaires alors (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont parallèles.
  • si n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } ne sont pas colinéaires alors (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) ne sont pas parallèles. Cela signifie donc que les plans sont sécants.
Soient n1→(214)\overrightarrow{n_{1} } \left(\begin{array}{c} {2} \\ {1} \\ {4} \end{array}\right) et n2→(420)\overrightarrow{n_{2} } \left(\begin{array}{c} {4} \\ {2} \\ {0} \end{array}\right) des vecteurs normaux respectifs des plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right).
On vérifie facilement que les deux vecteurs normaux ne sont pas colinéaires (non proportionnels), alors les plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) ne sont pas parallèles.
Question 4
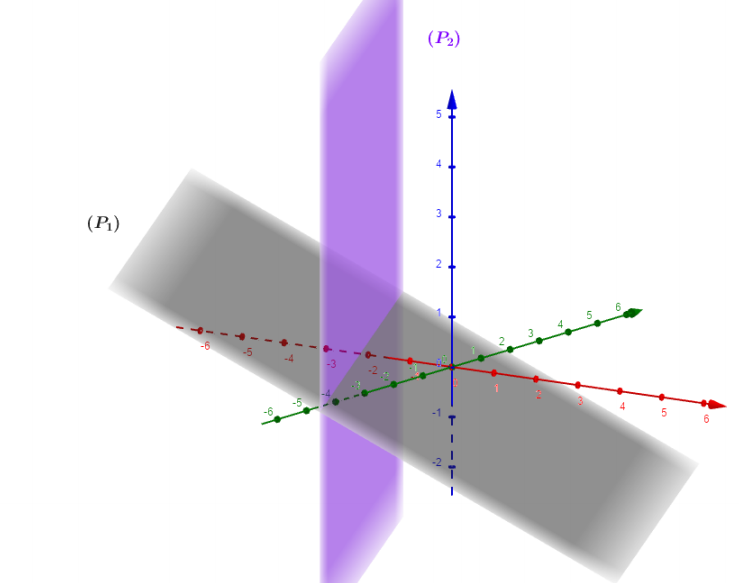
Dans l'espace muni d'un repère (O;i→;j→;k→)\left(O;\overrightarrow{i} ;\overrightarrow{j} ;\overrightarrow{k} \right), on considère les deux plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) admettant pour équation cartésienne
(P1):5x+2y+3z+4=0\left(P_{1} \right):5x+2y+3z+4=0 et (P2):3x+65y+95z−7=0\left(P_{2} \right):3x+\frac{6}{5}y+\frac{9}{5}z-7=0

(P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont-ils parallèles ?

Correction
    Soient n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } des vecteurs normaux respectifs des plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right).
  • si n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } sont colinéaires alors (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont parallèles.
  • si n1→\overrightarrow{n_{1} } et n2→\overrightarrow{n_{2} } ne sont pas colinéaires alors (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) ne sont pas parallèles. Cela signifie donc que les plans sont sécants.
Soient n1→(523)\overrightarrow{n_{1} } \left(\begin{array}{c} {5} \\ {2} \\ {3} \end{array}\right)et n2→(36595)\overrightarrow{n_{2} } \left(\begin{array}{c} {3} \\ {\frac{6}{5}} \\ {\frac{9}{5}} \end{array}\right) des vecteurs normaux respectifs des plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right).
On vérifie facilement que les deux vecteurs normaux sont colinéaires car :
n2→=35×n1→\overrightarrow{n_{2} }=\frac{3}{5}\times \overrightarrow{n_{1} }
, alors les plans (P1)\left(P_{1} \right) et (P2)\left(P_{2} \right) sont parallèles.