Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Calculer un produit scalaire de deux vecteurs dans l'espace - Exercice 4

9 min
20
Soit ABCDABCD un tétraèdre régulier d'arête 44 cm . JJ est le milieu de [AC]\left[AC\right] ; KK est le milieu de [AD]\left[AD\right] et II est le milieu de [BC]\left[BC\right] .
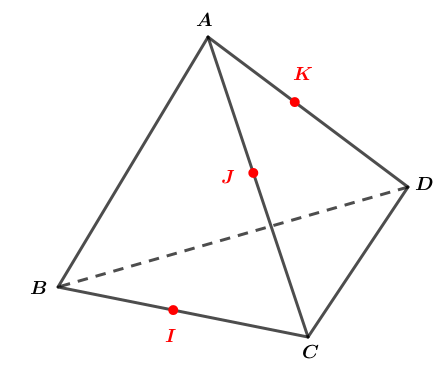
Question 1

Calculer CB→⋅CD→\overrightarrow{CB} \cdot \overrightarrow{CD}

Correction
ABCDABCD un tétraèdre régulier. Il en résulte donc que toutes les arêtes ont la même longueur c'est à dire 44 cm.
On peut donc affirmer que le triangle BCDBCD est un triangle équilatéral et que BCD^=π3\widehat{BCD}=\frac{\pi}{3} .
  • Le produit scalaire de deux vecteurs u→\overrightarrow{u} et v→\overrightarrow{v} non nuls est défini par :
    u→.v→=∥u→∥×∥v→∥×cos⁡(u⃗,v→)\overrightarrow{u} .\overrightarrow{v} =\left\| \overrightarrow{u} \right\| \times \left\| \overrightarrow{v} \right\| \times \cos \left(\vec{u} ,\overrightarrow{v} \right)
CB→⋅CD→=∥CB→∥×∥CD→∥×cos⁡(CB→,CD→)\overrightarrow{CB} \cdot \overrightarrow{CD} =\left\| \overrightarrow{CB} \right\| \times \left\| \overrightarrow{CD} \right\| \times \cos \left(\overrightarrow{CB} ,\overrightarrow{CD} \right)
CB→⋅CD→=4×4×cos⁡(π3)\overrightarrow{CB} \cdot \overrightarrow{CD} =4\times 4\times \cos \left(\frac{\pi}{3} \right)
CB→⋅CD→=16×12\overrightarrow{CB} \cdot \overrightarrow{CD} =16\times \frac{1 }{2}
CB→⋅CD→=8\overrightarrow{CB} \cdot \overrightarrow{CD} =8
Question 2

Calculer JK→⋅CD→\overrightarrow{JK} \cdot \overrightarrow{CD}

Correction
JJ est le milieu de [AC]\left[AC\right] et KK est le milieu de [AD]\left[AD\right] .
Théorème des milieux
  • Dans un triangle, si une droite passe par les milieux de deux côtés alors cette droite est parallèle au troisième côté.
  • Dans un triangle, si un segment a pour extrémités les milieux de deux côtés du triangle alors il mesure la moitié du troisième côté.
On peut donc conclure que JK=12CDJK=\frac{1}{2}CD et également que JK→=12CD→\overrightarrow{JK} =\frac{1}{2} \overrightarrow{CD}
On peut donc écrire que :
JK→⋅CD→=12CD→⋅CD→\overrightarrow{JK} \cdot \overrightarrow{CD} =\frac{1}{2} \overrightarrow{CD} \cdot \overrightarrow{CD}
  • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de même sens alors : AB→⋅AC→=AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =AB\times AC
  • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de sens opposés alors : AB→⋅AC→=−AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =-AB\times AC
Les vecteurs CD→\overrightarrow{CD} et CD→\overrightarrow{CD} sont colinéaires mais ont des sens opposés.
Il vient alors que :
JK→⋅CD→=12×CD×CD\overrightarrow{JK} \cdot \overrightarrow{CD} =\frac{1}{2} \times CD\times CD
JK→⋅CD→=12×4×4\overrightarrow{JK} \cdot \overrightarrow{CD} =\frac{1}{2} \times 4\times 4
JK→⋅CD→=12×16\overrightarrow{JK} \cdot \overrightarrow{CD} =\frac{1}{2} \times 16
Ainsi :
JK→⋅CD→=8\overrightarrow{JK} \cdot \overrightarrow{CD} =8
Question 3

Calculer AI→⋅BC→\overrightarrow{AI} \cdot \overrightarrow{BC}

Correction
La droite (AI)\left(AI\right) est une médiane du triangle ABCABC.
  • Dans un triangle équilatéral, toutes les droites remarquables (médiane, hauteur, bissectrice, médiatrice) relatives à un même côté sont confondues.
Il en résulte donc que la droite (AI)\left(AI\right) est également une hauteur du triangle ABCABC. Plus précisément, la droite (AI)\left(AI\right) est une hauteur issue de AA. On peut alors affirmer que les droites (AI)\left(AI\right) et (BC)\left(BC\right) sont perpendiculaires\red{\text{perpendiculaires}}.
Ainsi :
AI→⋅BC→=0\overrightarrow{AI} \cdot \overrightarrow{BC} =0

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.