Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Comment reconnaître qu'une fonction admet une asymptote horizontale ou une asymptote verticale - Exercice 1
20 min
35
Calculer les limites suivantes.
Que peut-on en déduire graphiquement ?
Que peut-on en déduire graphiquement ?
Question 1
Correction
Si où est une valeur finie alors la fonction admet une asymptote horizontale d'équation
Si où est une valeur finie alors la fonction admet une asymptote horizontale d'équation
par quotient : Si où est une valeur finie alors la fonction admet une asymptote horizontale d'équation
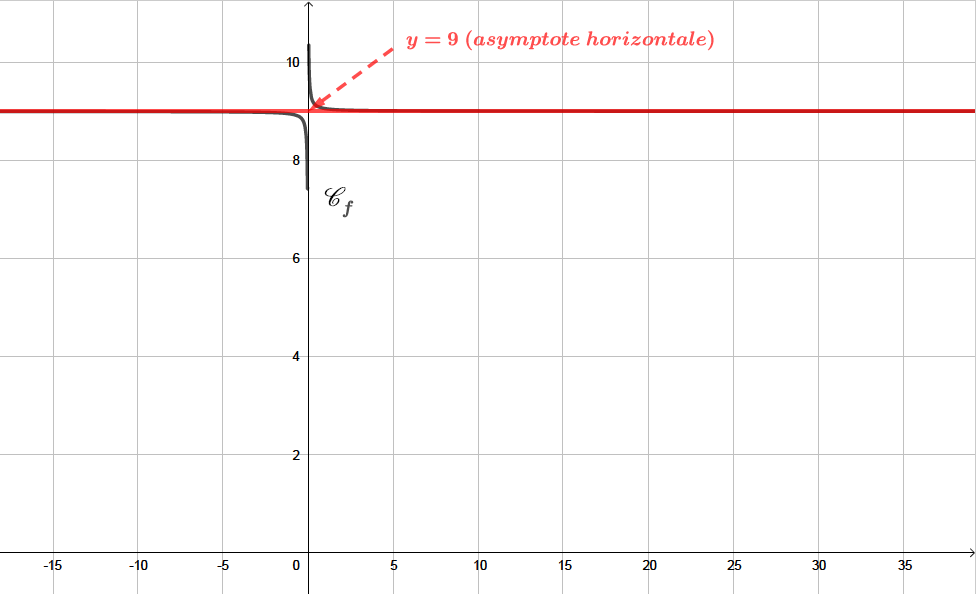
La courbe admet au voisinage de une asymptote horizontale d'équation .
Si on rencontre une forme alors la limite sera égale à zéro.
Question 2
Correction
Si où est une valeur finie alors la fonction admet une asymptote horizontale d'équation
Si où est une valeur finie alors la fonction admet une asymptote horizontale d'équation
ainsi Si où est une valeur finie alors la fonction admet une asymptote horizontale d'équation
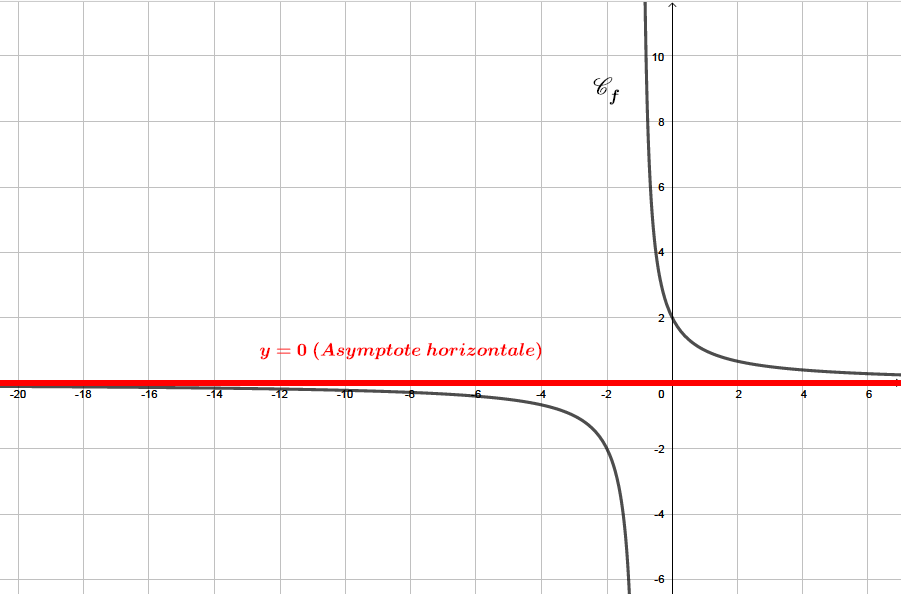
La courbe admet au voisinage de une asymptote horizontale d'équation .
Question 3
Correction
Si où est une valeur finie alors la fonction admet une asymptote horizontale d'équation
Si où est une valeur finie alors la fonction admet une asymptote horizontale d'équation
on obtient une forme indéterminée Si où est une valeur finie alors la fonction admet une asymptote horizontale d'équation
On va factoriser le numérateur par le monôme de plus haut degré c'est à dire par et le dénominateur par le monôme de plus haut degré c'est à dire par
Il vient :
Ainsi : par quotient :
Finalement :
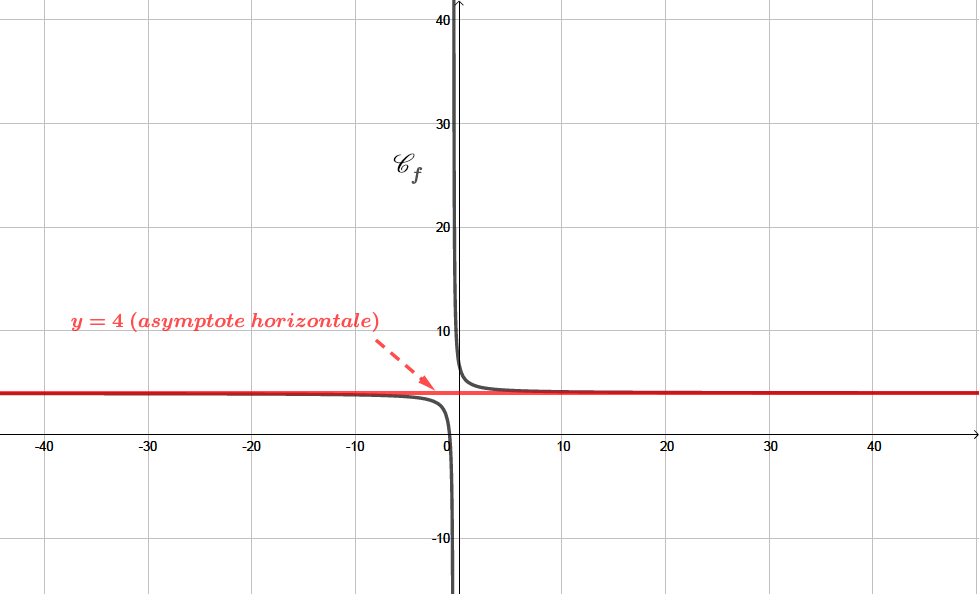
La courbe admet au voisinage de une asymptote horizontale d'équation .
On rappelle que : .
Question 4
Correction
Si où est une valeur finie alors la fonction admet une asymptote horizontale d'équation
Si où est une valeur finie alors la fonction admet une asymptote horizontale d'équation
on obtient une forme indéterminée Si où est une valeur finie alors la fonction admet une asymptote horizontale d'équation
On va factoriser le numérateur par le monôme de plus haut degré c'est à dire par et le dénominateur par le monôme de plus haut degré c'est à dire par
Il vient :
.
On simplifie le numérateur et le dénominateur par .
Ainsi : par quotient :
Finalement :
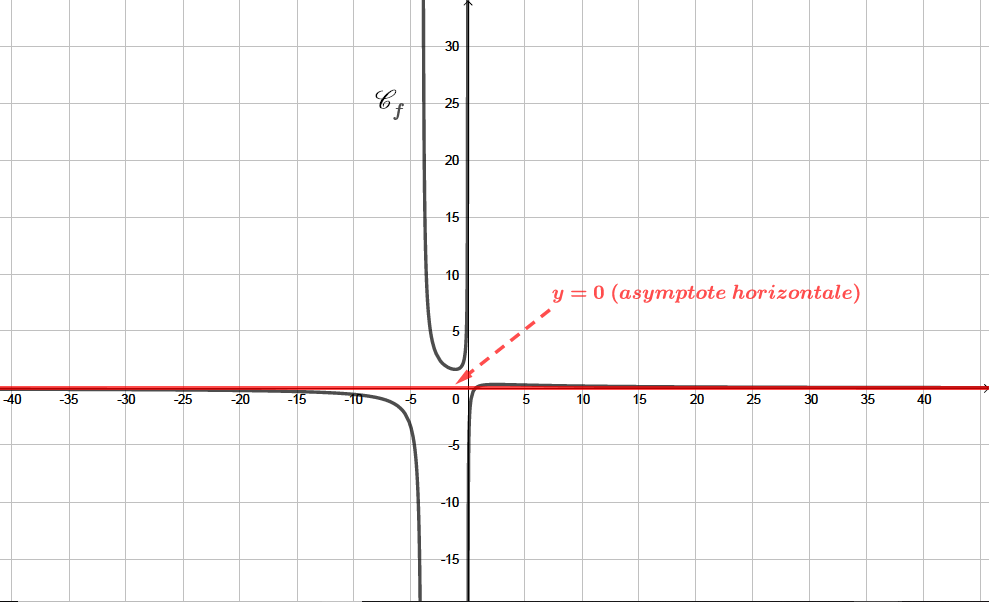
La courbe admet au voisinage de une asymptote horizontale d'équation .

Question 5
Correction
Si où est une valeur finie alors la fonction admet une asymptote horizontale d'équation
Si où est une valeur finie alors la fonction admet une asymptote horizontale d'équation
Si où est une valeur finie alors la fonction admet une asymptote horizontale d'équation
Il s'agit d'une limite par composition.
On commence par calculer .
Ainsi :
On pose .
Lorsque tend vers alors tend vers .
Or :
Par composition :
La courbe admet au voisinage de une asymptote horizontale d'équation .