Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Repères et coordonnées - Exercice 1

15 min
25
Soit ABCDABCD un tétraèdre. On considère les points II et JJ milieux respectifs de [AC]\left[AC\right] et [BD]\left[BD\right].
Les points P,Q,RP,Q,R et SS sont définis par
AP→=25AB→\overrightarrow{AP} =\frac{2}{5} \overrightarrow{AB} , AQ→=23AD→\overrightarrow{AQ} =\frac{2}{3} \overrightarrow{AD} , CR→=13CB→\overrightarrow{CR} =\frac{1}{3} \overrightarrow{CB} et CS→=25CD→\overrightarrow{CS} =\frac{2}{5} \overrightarrow{CD}
On considère le repère (A;AB→;AC→;AD→)\left(A;\overrightarrow{AB} ;\overrightarrow{AC} ;\overrightarrow{AD} \right)
Question 1

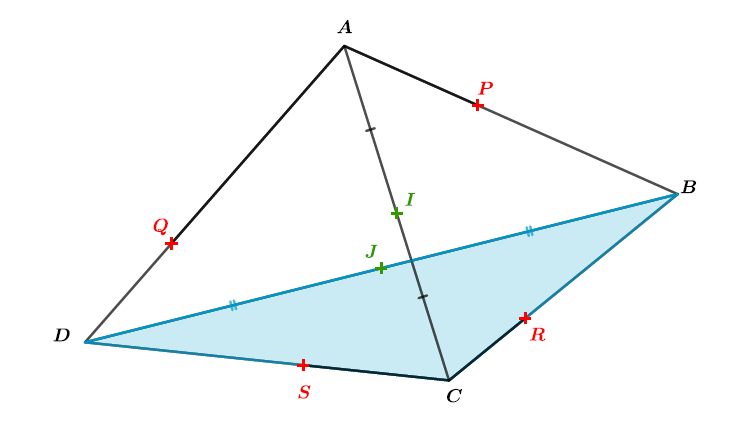
Déterminer les coordonnées des points A,B,CA,B,C et DD.

Correction
On considère le repère (A;AB→;AC→;AD→)\left(A;\overrightarrow{AB} ;\overrightarrow{AC} ;\overrightarrow{AD} \right). Si l'on veut déterminer les coordonnées par exemple d'un point MM il faut l'exprimer le point MM avec l'origine du repère en fonction des vecteurs du repère donné. Dans notre exemple, si AM→=xAB→+yAC→+zAD→\overrightarrow{AM} =\red{x}\overrightarrow{AB} +\blue{y}\overrightarrow{AC} +\purple{z}\overrightarrow{AD} alors les coordonnées de MM sont (x;y;z)\left(\red{x};\blue{y};\purple{z}\right)
AA est l'origine du repère ainsi A(0;0;0)A\left(0;0;0\right)
  • AB→=1AB→+0AC→+0AD→\overrightarrow{AB} =\red{1}\overrightarrow{AB} +\blue{0}\overrightarrow{AC} +\purple{0}\overrightarrow{AD} donc les coordonnées de BB sont (1;0;0)\left(\red{1};\blue{0};\purple{0}\right)
  • AC→=0AB→+1AC→+0AD→\overrightarrow{AC} =\red{0}\overrightarrow{AB} +\blue{1}\overrightarrow{AC} +\purple{0}\overrightarrow{AD} donc les coordonnées de CC sont (0;1;0)\left(\red{0};\blue{1};\purple{0}\right)
  • AD→=0AB→+0AC→+1AD→\overrightarrow{AD} =\red{0}\overrightarrow{AB} +\blue{0}\overrightarrow{AC} +\purple{1}\overrightarrow{AD} donc les coordonnées de DD sont (0;0;1)\left(\red{0};\blue{0};\purple{1}\right)
    • Question 2

    Déterminer les coordonnées des points PP  \;et  \;QQ .

    Correction
    On considère le repère (A;AB→;AC→;AD→)\left(A;\overrightarrow{AB} ;\overrightarrow{AC} ;\overrightarrow{AD} \right). Si l'on veut déterminer les coordonnées par exemple d'un point MM il faut l'exprimer le point MM avec l'origine du repère en fonction des vecteurs du repère donné. Dans notre exemple, si AM→=xAB→+yAC→+zAD→\overrightarrow{AM} =\red{x}\overrightarrow{AB} +\blue{y}\overrightarrow{AC} +\purple{z}\overrightarrow{AD} alors les coordonnées de MM sont (x;y;z)\left(\red{x};\blue{y};\purple{z}\right)
    AA est l'origine du repère ainsi A(0;0;0)A\left(0;0;0\right) . D'après les hypothèses nous savons que : AP→=25AB→\overrightarrow{AP} =\frac{2}{5} \overrightarrow{AB}   \; et   \;AQ→=23AD→\overrightarrow{AQ} =\frac{2}{3} \overrightarrow{AD} . Il vient alors que :
  • AP→=25AB→+0AC→+0AD→\overrightarrow{AP} =\red{\frac{2}{5}} \overrightarrow{AB} +\blue{0}\overrightarrow{AC} +\purple{0}\overrightarrow{AD} donc les coordonnées de PP sont (25;0;0)\left(\red{\frac{2}{5}} ;\blue{0};\purple{0}\right)
  • AQ→=0AB→+0AC→+23AD→\overrightarrow{AQ} =\red{0}\overrightarrow{AB} +\blue{0}\overrightarrow{AC} +\purple{\frac{2}{3} }\overrightarrow{AD} donc les coordonnées de QQ sont (0;0;23)\left(\red{0};\blue{0};\purple{\frac{2}{3} } \right)
    • Question 3

    Déterminer les coordonnées du point RR.

    Correction
    On considère le repère (A;AB→;AC→;AD→)\left(A;\overrightarrow{AB} ;\overrightarrow{AC} ;\overrightarrow{AD} \right). Si l'on veut déterminer les coordonnées par exemple d'un point MM il faut l'exprimer le point MM avec l'origine du repère en fonction des vecteurs du repère donné. Dans notre exemple, si AM→=xAB→+yAC→+zAD→\overrightarrow{AM} =\red{x}\overrightarrow{AB} +\blue{y}\overrightarrow{AC} +\purple{z}\overrightarrow{AD} alors les coordonnées de MM sont (x;y;z)\left(\red{x};\blue{y};\purple{z}\right)
    D'après les hypothèses, nous savons que : CR→=13CB→\overrightarrow{CR} =\frac{1}{3} \overrightarrow{CB}
  • CR→=13CB→\overrightarrow{CR} =\frac{1}{3} \overrightarrow{CB} avec la relation de Chasles on a : CR→=13(CA→+AB→)=13CA→+13AB→\overrightarrow{CR} =\frac{1}{3} \left(\overrightarrow{CA} +\overrightarrow{AB} \right)=\frac{1}{3} \overrightarrow{CA} +\frac{1}{3} \overrightarrow{AB}
    Soit : CR→=13AB→−13AC→+0AD→\overrightarrow{CR} =\frac{1}{3} \overrightarrow{AB} -\frac{1}{3} \overrightarrow{AC} +0\overrightarrow{AD} .
    Ensuite il ne faut pas oublier d'exprimer CR→\overrightarrow{CR} avec l'origine du repère, ce qui donne CA→+AR→=13AB→−13AC→+0AD→\overrightarrow{CA} +\overrightarrow{AR} =\frac{1}{3} \overrightarrow{AB} -\frac{1}{3} \overrightarrow{AC} +0\overrightarrow{AD} .
    On a alors :
    AR→=13AB→−13AC→−CA→+0AD→\overrightarrow{AR} =\frac{1}{3} \overrightarrow{AB} -\frac{1}{3} \overrightarrow{AC} -\overrightarrow{CA} +0\overrightarrow{AD}
    AR→=13AB→−13AC→+AC→+0AD→\overrightarrow{AR} =\frac{1}{3} \overrightarrow{AB} -\frac{1}{3} \overrightarrow{AC} +\overrightarrow{AC} +0\overrightarrow{AD}
    Enfin : AR→=13AB→+23AC→+0AD→\overrightarrow{AR} =\red{\frac{1}{3}} \overrightarrow{AB} +\blue{\frac{2}{3}} \overrightarrow{AC} +\purple{0}\overrightarrow{AD} donc les coordonnées de RR sont (13;23;0)\left(\red{\frac{1}{3}} ;\blue{\frac{2}{3}} ;\purple{0}\right)
    • Question 4

    Déterminer les coordonnées du point SS.

    Correction
    On considère le repère (A;AB→;AC→;AD→)\left(A;\overrightarrow{AB} ;\overrightarrow{AC} ;\overrightarrow{AD} \right). Si l'on veut déterminer les coordonnées par exemple d'un point MM il faut l'exprimer le point MM avec l'origine du repère en fonction des vecteurs du repère donné. Dans notre exemple, si AM→=xAB→+yAC→+zAD→\overrightarrow{AM} =\red{x}\overrightarrow{AB} +\blue{y}\overrightarrow{AC} +\purple{z}\overrightarrow{AD} alors les coordonnées de MM sont (x;y;z)\left(\red{x};\blue{y};\purple{z}\right)
  • On sait que CS→=25CD→\overrightarrow{CS} =\frac{2}{5} \overrightarrow{CD} , donc d'après la relation de Chasles :
    CA→+AS→=25CD→\overrightarrow{CA} +\overrightarrow{AS} =\frac{2}{5} \overrightarrow{CD} .
    Soit : AS→=25CD→−CA→\overrightarrow{AS} =\frac{2}{5} \overrightarrow{CD} -\overrightarrow{CA} .
    On effectue la relation de Chasles avec le vecteur CD→\overrightarrow{CD} , il en résulte que :
    AS→=25(CA→+AD→)−CA→\overrightarrow{AS} =\frac{2}{5} \left(\overrightarrow{CA} +\overrightarrow{AD} \right)-\overrightarrow{CA}
    AS→=25CA→+25AD→−CA→ \overrightarrow{AS} =\frac{2}{5} \overrightarrow{CA} +\frac{2}{5} \overrightarrow{AD} -\overrightarrow{CA}
    AS→=−35CA→+25AD→ \overrightarrow{AS} =-\frac{3}{5} \overrightarrow{CA} +\frac{2}{5} \overrightarrow{AD}
    Enfin : AS→=0AB→+35AC→+25AD→ \overrightarrow{AS} =\red{0}\overrightarrow{AB} +\blue{\frac{3}{5}} \overrightarrow{AC} +\purple{\frac{2}{5}} \overrightarrow{AD}
    Donc les coordonnées de SS sont (0;35;25)\left(\red{0};\blue{\frac{3}{5}} ;\purple{\frac{2}{5}} \right)
    • Question 5

    Déterminer les coordonnées des points II et JJ .

    Correction
    Les points II et JJ sont les milieux respectifs de [AC]\left[AC\right] et [BD]\left[BD\right].
    Nous savons également que : A(0;0;0)A\left(0;0;0\right) , B(1;0;0)B\left(\red{1};\blue{0};\purple{0}\right) , C(0;1;0)C\left(\red{0};\blue{1};\purple{0}\right) et D(0;0;1)D\left(\red{0};\blue{0};\purple{1}\right)
  • Calculons les coordonnées de II et JJ.
    D’une part :\red{\text{D'une part :}} les coordonnées de II sont données par
    xI=xA+xC2⇔xI=0+02⇔xI=0x_{I} =\frac{x_{A} +x_{C} }{2} \Leftrightarrow x_{I} =\frac{0+0}{2} \Leftrightarrow x_{I} =0
    yI=yA+yC2⇔yI=0+12⇔yI=12y_{I} =\frac{y_{A} +y_{C} }{2} \Leftrightarrow y_{I} =\frac{0+1}{2} \Leftrightarrow y_{I} =\frac{1}{2}
    zI=zA+zC2⇔zI=0+02⇔zI=0z_{I} =\frac{z_{A} +z_{C} }{2} \Leftrightarrow z_{I} =\frac{0+0}{2} \Leftrightarrow z_{I} =0
    Les coordonnées de II sont alors (0;12;0)\left(0;\frac{1}{2} ;0\right)
    • D’autre part :\red{\text{D'autre part :}} les coordonnées de JJ sont données par
    xJ=xB+xD2⇔xJ=1+02⇔xJ=12x_{J} =\frac{x_{B} +x_{D} }{2} \Leftrightarrow x_{J} =\frac{1+0}{2} \Leftrightarrow x_{J} =\frac{1}{2}
    yJ=yB+yD2⇔yJ=0+02⇔yJ=0y_{J} =\frac{y_{B} +y_{D} }{2} \Leftrightarrow y_{J} =\frac{0+0}{2} \Leftrightarrow y_{J} =0
    zJ=zB+zD2⇔zI=0+12⇔zI=12z_{J} =\frac{z_{B} +z_{D} }{2} \Leftrightarrow z_{I} =\frac{0+1}{2} \Leftrightarrow z_{I} =\frac{1}{2}
    Les coordonnées de JJ sont alors (12;0;12)\left(\frac{1}{2} ;0;\frac{1}{2} \right)