Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Montrer que des vecteurs forment une base - Exercice 1

3 min
5
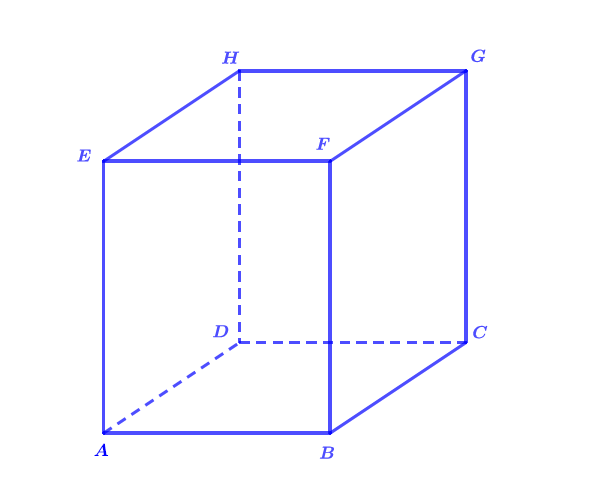
On considère le cube ABCDEFGHABCDEFGH ci-dessous :
Question 1

Justifier que (AB→,AD→,AE→)\left(\overrightarrow{AB} ,\overrightarrow{AD} ,\overrightarrow{AE} \right) est une base de l'espace.

Correction
  • On appelle base\blue{\text{base}} de l'espace tout triplet (u→,v→,w→)\left(\overrightarrow{u} ,\overrightarrow{v} ,\overrightarrow{w} \right) de vecteurs non coplanaires.
    • Le point EE n'appartient pas au plan (BAD)\left(BAD\right).
    Il en résulte donc que les vecteurs AB→,  AD→\overrightarrow{AB} ,\;\overrightarrow{AD} et AE→\overrightarrow{AE} ne sont pas coplanaires\red{\text{ne sont pas coplanaires}}.
    On peut alors conclure que (AB→,AD→,AE→)\left(\overrightarrow{AB} ,\overrightarrow{AD} ,\overrightarrow{AE} \right) est bien une base de l'espace.
    Question 2

    Justifier que (A;AB→,AD→,AE→)\left(A;\overrightarrow{AB} ,\overrightarrow{AD} ,\overrightarrow{AE} \right) est un repère de l'espace.

    Correction
  • Un repeˋre\blue{\text{repère}} de l'espace est un quadruplet (O;u→,v→,w→)\left(O;\overrightarrow{u} ,\overrightarrow{v} ,\overrightarrow{w} \right) dans lequel OO est un point appelé origine du repère et u→,  v→\overrightarrow{u} ,\;\overrightarrow{v} et w→\overrightarrow{w} sont trois vecteurs non coplanaires.
    • D'après la question précédente, nous avons montré que (AB→,AD→,AE→)\left(\overrightarrow{AB} ,\overrightarrow{AD} ,\overrightarrow{AE} \right) est bien une base de l'espace.
    Il en résulte donc que (A;AB→,AD→,AE→)\left(A;\overrightarrow{AB} ,\overrightarrow{AD} ,\overrightarrow{AE} \right) est un repère de l'espace, dans lequel AA est un point appelé origine du repère et AB→,  AD→\overrightarrow{AB} ,\;\overrightarrow{AD} et AE→\overrightarrow{AE} sont trois vecteurs non coplanaires.