Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Savoir étudier le signe avec les formes et - Exercice 1
15 min
25
Question 1
Etudier le signe de la fonction sur l'intervalle .
Correction
Pour étudier le signe de la fonction . Il faut suivre les étapes suivantes :
1ère étape : Résolution de l'équation .
équivaut successivement à :
. Or . D'où :
avec . Ce sont les solutions sur .
avec . équivaut successivement à :
avec .
avec .
avec .
Les solutions de l'équation sur l'intervalle sont et .
2ème étape : Etude du signe de .
Nous travaillons sur l'intervalle .
Comme alors et ainsi : .
Or nous savons que la fonction sinus est sur l'intervalle .
De ce fait comme alors .
Il en résulte donc que la fonction est sur l'intervalle .
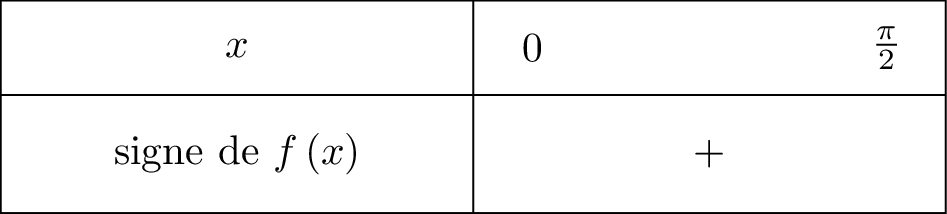
1ère étape : Résolution de l'équation .
équivaut successivement à :
. Or . D'où :
avec . Ce sont les solutions sur .
avec .
avec .
avec .
Les solutions de l'équation sur l'intervalle sont et .
2ème étape : Etude du signe de .
Nous travaillons sur l'intervalle .
Comme alors et ainsi : .
Or nous savons que la fonction sinus est sur l'intervalle .
De ce fait comme alors .
Il en résulte donc que la fonction est sur l'intervalle .

Question 2
Etudier le signe de la fonction sur l'intervalle .
Correction
Pour étudier le signe de la fonction . Il faut suivre les étapes suivantes :
1ère étape : Résolution de l'équation .
équivaut successivement à :
. Or . D'où :
avec . Ce sont les solutions sur .
avec . équivaut successivement à :
avec .
avec .
L'unique solution de l'équation sur l'intervalle est .
2ème étape : Etude du signe de .
Nous travaillons sur l'intervalle .
La fonction s'annule uniquement pour sur l'intervalle .
Nous allons donc étudier le signe de la fonction sur l'intervalle puis ensuite sur l'intervalle .
alors et ainsi : . Or nous savons que la fonction cosinus est sur l'intervalle .
De ce fait comme alors . alors et ainsi : . D'où : . Or nous savons que la fonction cosinus est sur l'intervalle .
De ce fait comme alors . Nous dressons ci-dessous le tableau de signe de sur l'intervalle .

1ère étape : Résolution de l'équation .
équivaut successivement à :
. Or . D'où :
avec . Ce sont les solutions sur .
avec .
avec .
L'unique solution de l'équation sur l'intervalle est .
2ème étape : Etude du signe de .
Nous travaillons sur l'intervalle .
La fonction s'annule uniquement pour sur l'intervalle .
Nous allons donc étudier le signe de la fonction sur l'intervalle puis ensuite sur l'intervalle .
De ce fait comme alors .
De ce fait comme alors .
