Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Résoudre des inéquations trigonométriques - Exercice 1
30 min
50
Question 1
Résoudre l'inéquation suivante : sur l'intervalle
Correction
résoudre l'équation sur l'intervalle
Or , ainsi
avec . Ici, ce sont les solutions sur .
Enfin les solutions sur sont .
La méthode est détaillée à l'exercice 4 et cf vidéo équation et trigonométrie.
on résout puis on va utiliser le cercle trigonométrique.
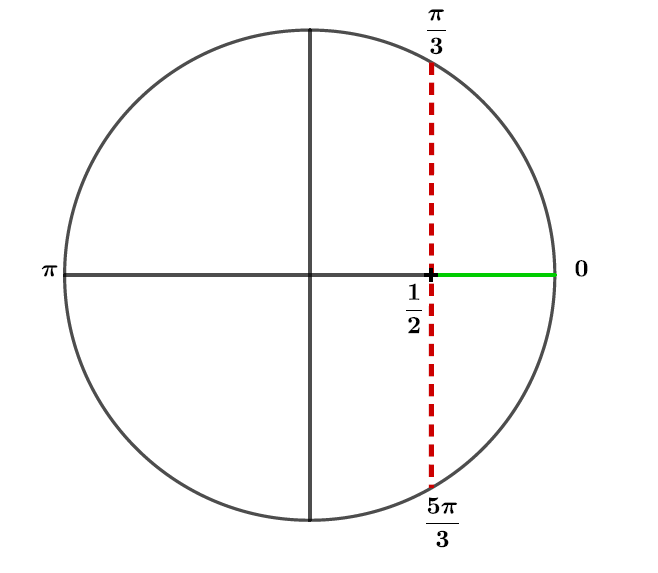 Le segment vert représente la zone où . Ainsi entre et on aura , c'est-à-dire qui est équivalent à :
Le segment vert représente la zone où . Ainsi entre et on aura , c'est-à-dire qui est équivalent à :
On intègre cela dans un tableau de signe ci-dessous. Il vient alors :
 Les solutions de l'inéquation sont :
Les solutions de l'inéquation sont :
Or , ainsi
avec . Ici, ce sont les solutions sur .
Enfin les solutions sur sont .
La méthode est détaillée à l'exercice 4 et cf vidéo équation et trigonométrie.
on résout puis on va utiliser le cercle trigonométrique.

On intègre cela dans un tableau de signe ci-dessous. Il vient alors :

Question 2
Résoudre l'inéquation suivante : sur l'intervalle
Correction
résoudre l'équation sur l'intervalle
Or , ainsi
avec .
Ainsi
Enfin les solutions sur sont
La méthode est détaillée à l'exercice 4 et cf vidéo équation et trigonométrie.
on résout puis on va utiliser le cercle trigonométrique.
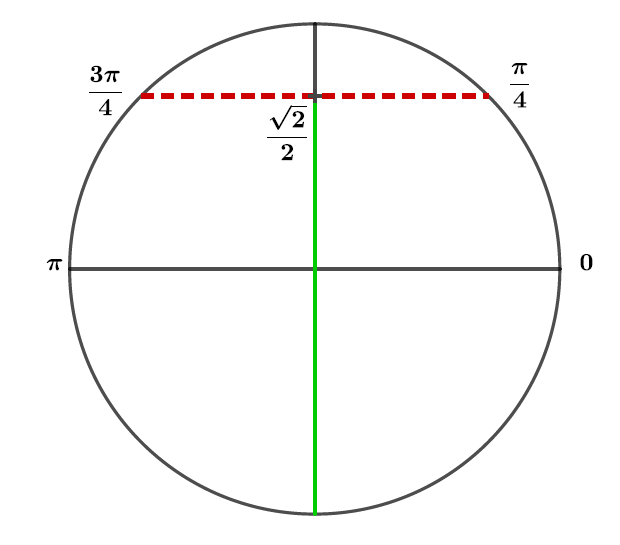 Le segment vert représente la zone où . Ainsi entre et on aura , c'est-à-dire .
Le segment vert représente la zone où . Ainsi entre et on aura , c'est-à-dire .
On intègre cela dans un tableau de signe ci-dessous. Il vient alors :
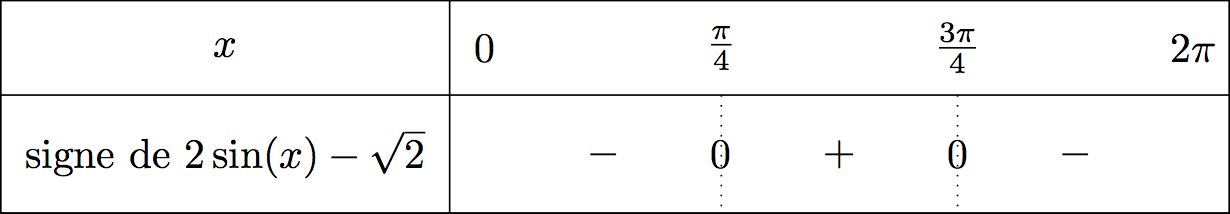 Les solutions de l'inéquation sont :
Les solutions de l'inéquation sont :
Or , ainsi
avec .
Ainsi
Enfin les solutions sur sont
La méthode est détaillée à l'exercice 4 et cf vidéo équation et trigonométrie.
on résout puis on va utiliser le cercle trigonométrique.

On intègre cela dans un tableau de signe ci-dessous. Il vient alors :
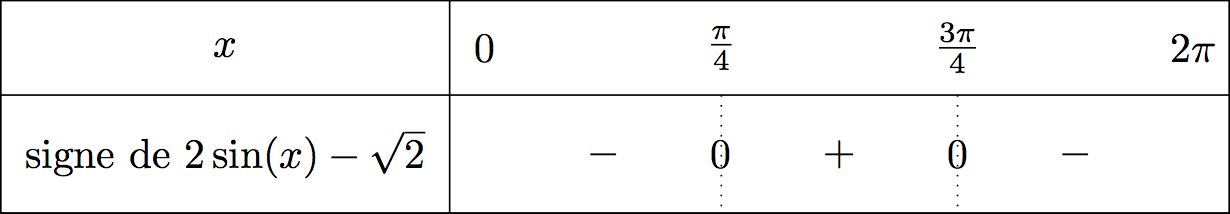
Question 3
Résoudre l'inéquation suivante : sur l'intervalle
Correction
résoudre l'équation sur l'intervalle
Or , ainsi
avec . Ici, ce sont les solutions sur .
Enfin les solutions sur sont La méthode est détaillée à l'exercice 4 et cf vidéo équation et trigonométrie.
on résout puis on va utiliser le cercle trigonométrique.
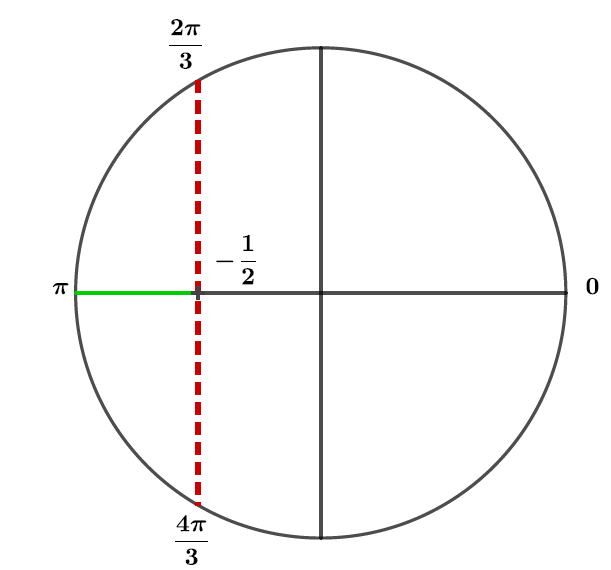 Le segment vert représente la zone où . Ainsi sur l'intervalle on aura , c'est-à-dire .
Le segment vert représente la zone où . Ainsi sur l'intervalle on aura , c'est-à-dire .
On intègre cela dans un tableau de signe ci-dessous. Il vient alors : Les solutions de l'inéquation sont :
Les solutions de l'inéquation sont :
Or , ainsi
avec . Ici, ce sont les solutions sur .
Enfin les solutions sur sont La méthode est détaillée à l'exercice 4 et cf vidéo équation et trigonométrie.
on résout puis on va utiliser le cercle trigonométrique.

On intègre cela dans un tableau de signe ci-dessous. Il vient alors :

Question 4
Résoudre l'inéquation suivante : sur l'intervalle
Correction
résoudre l'équation sur l'intervalle
Or , ainsi
avec .
Ainsi
Enfin les solutions sur sont
La méthode est détaillée à l'exercice 4 et la vidéo équation et trigonométrie.
on résout puis on va utiliser le cercle trigonométrique.
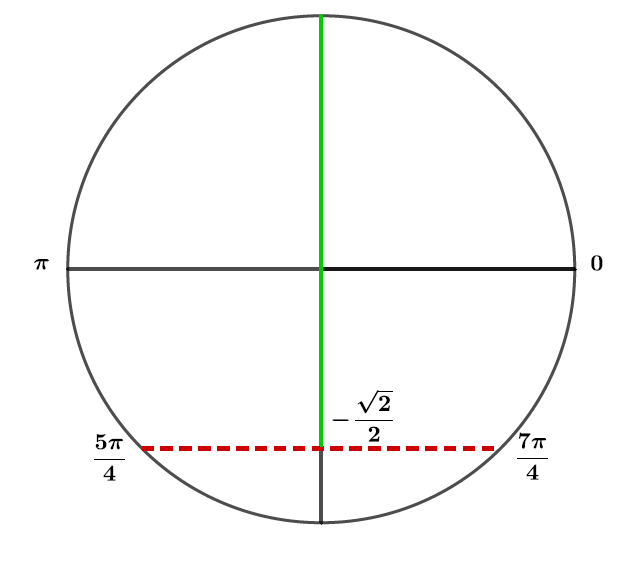 Le segment vert représente la zone où . Ainsi entre et on aura , c'est-à-dire .
Le segment vert représente la zone où . Ainsi entre et on aura , c'est-à-dire .
On intègre cela dans un tableau de signe ci-dessous. Il vient alors :
 Les solutions de l'inéquation sont :
Les solutions de l'inéquation sont :
Or , ainsi
avec .
Ainsi
Enfin les solutions sur sont
La méthode est détaillée à l'exercice 4 et la vidéo équation et trigonométrie.
on résout puis on va utiliser le cercle trigonométrique.

On intègre cela dans un tableau de signe ci-dessous. Il vient alors :

Question 5
Résoudre l'inéquation suivante : sur l'intervalle .
Correction
Résoudre l'équation sur l'intervalle
Or , ainsi
avec . Ce sont les solutions sur .
avec . Ici, ce sont les solutions sur .
Enfin les solutions sur sont
On résout puis on va utiliser le cercle trigonométrique.
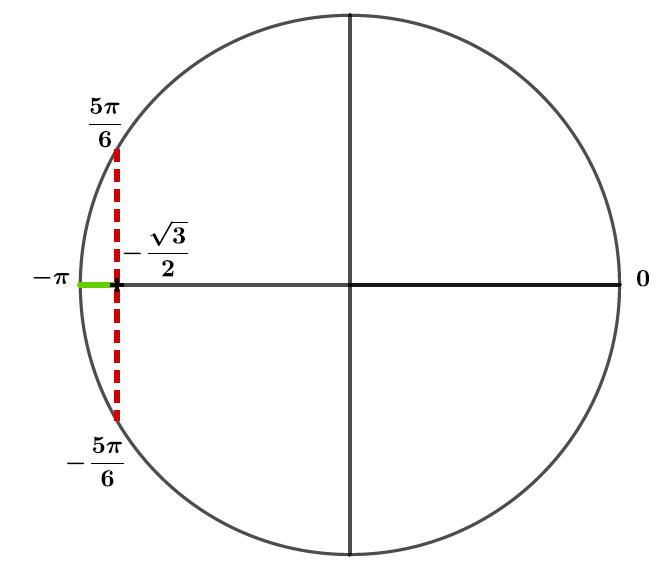
Le segment vert représente la zone où .
Ainsi entre et on aura :
, c'est-à-dire .
On intègre cela dans un tableau de signe ci-dessous. Il vient alors :
 Les solutions de l'inéquation sont
Les solutions de l'inéquation sont
Or , ainsi
avec . Ce sont les solutions sur .
Enfin les solutions sur sont
On résout puis on va utiliser le cercle trigonométrique.

Le segment vert représente la zone où .
Ainsi entre et on aura :
, c'est-à-dire .
On intègre cela dans un tableau de signe ci-dessous. Il vient alors :

Question 6
Résoudre l'inéquation suivante : sur l'intervalle
Correction
résoudre l'équation sur l'intervalle
Or , ainsi
avec .
Ainsi
Enfin les solutions sur sont
La méthode est détaillée à l'exercice 4 et la vidéo équation et trigonométrie.
on résout puis on va utiliser le cercle trigonométrique.
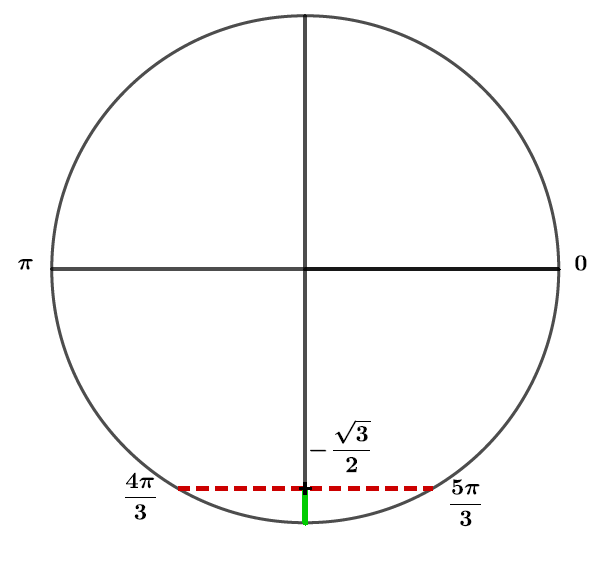 Le segment vert représente la zone où .
Le segment vert représente la zone où .
Ainsi sur l'intervalle on aura :
, c'est-à-dire .
On intègre cela dans un tableau de signe ci-dessous. Il vient alors :
 Les solutions de l'inéquation sont
Les solutions de l'inéquation sont
Or , ainsi
avec .
Ainsi
Enfin les solutions sur sont
La méthode est détaillée à l'exercice 4 et la vidéo équation et trigonométrie.
on résout puis on va utiliser le cercle trigonométrique.

Ainsi sur l'intervalle on aura :
, c'est-à-dire .
On intègre cela dans un tableau de signe ci-dessous. Il vient alors :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.