Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie - Exercice 1
20 min
35
Question 1
Soit la fonction définie par
Justifier que est définie sur .
Correction
est une fonction rationnelle, donc elle définie pour toutes les valeurs sauf pour celles qui l'annulent.
Or nous savons que :
ainsi et de ce fait : .
Cela signifie que le dénominateur ne s'annule jamais.
La fonction est bien définie sur .
Or nous savons que :
ainsi et de ce fait : .
Cela signifie que le dénominateur ne s'annule jamais.
La fonction est bien définie sur .
Question 2
Etudier la parité de .
Correction
est une fonction paire si pour tout réel , on a .
La fonction cosinus est paire.
est une fonction impaire si pour tout réel , on a .
La fonction sinus est impaire.
Attention, une fonction non paire n'est pas obligatoirement impaire et une fonction non impaire n'est pas obligatoirement paire.
Une fonction peut être ni paire, ni impaire.
La fonction est une fonction impaire.
Question 3
Calculer .
Correction
Soit .
est dérivable sur .
On reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
est dérivable sur .
On reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Question 4
En déduire les variations de sur .
Correction
Nous savons d'après la question précédente, que :
Pour tout réel , on peut affirmer que . De ce fait, le signe de ne dépend que de son dénominateur .
On va procéder en deux étapes.
Etape 1 : on commence par calculer : .
Or , ainsi
avec .
Ici, ce sont les solutions sur .
Les solutions sur l'intervalle sont .
Etape 2 : on résout : puis on va utiliser le cercle trigonométrique.
.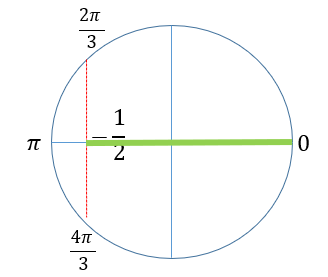 Le segment vert représente la zone où . Ainsi entre et on aura , c'est-à-dire . Nous traduisons cela dans le tableau de variation ci-dessous :
Le segment vert représente la zone où . Ainsi entre et on aura , c'est-à-dire . Nous traduisons cela dans le tableau de variation ci-dessous :
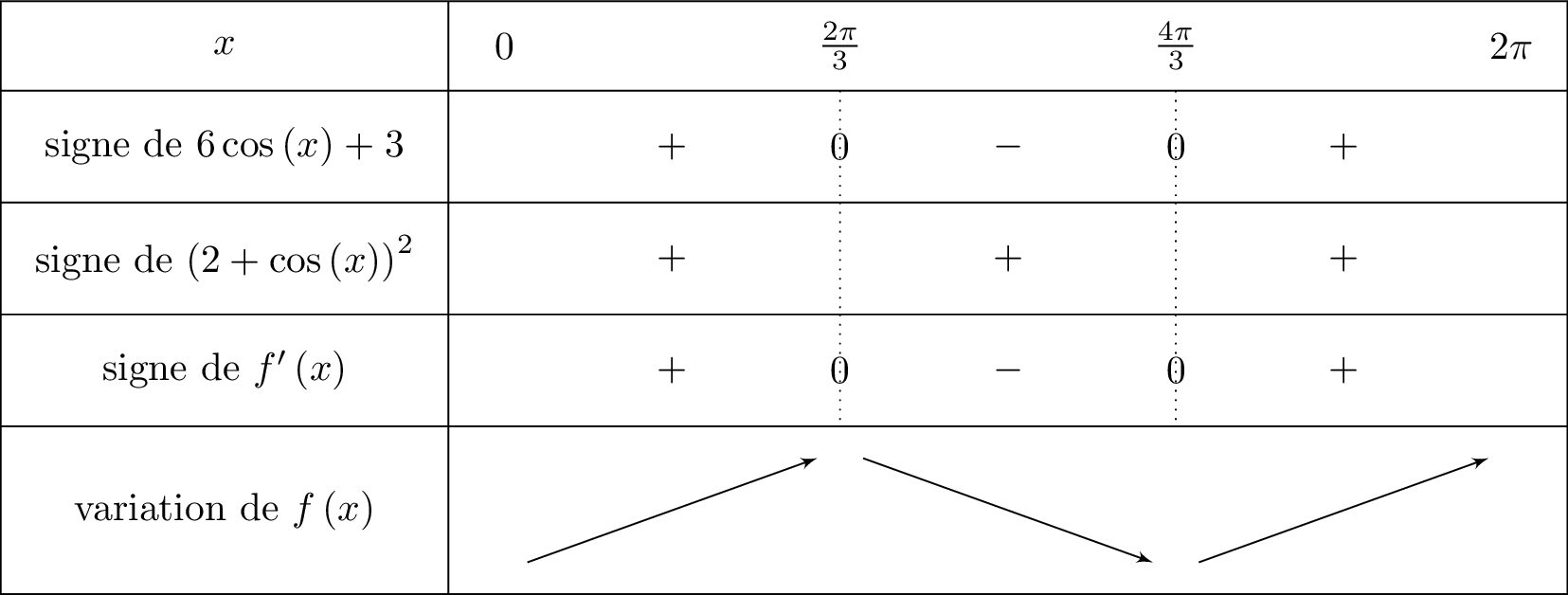
Pour tout réel , on peut affirmer que . De ce fait, le signe de ne dépend que de son dénominateur .
On va procéder en deux étapes.
Etape 1 : on commence par calculer : .
Or , ainsi
avec .
Ici, ce sont les solutions sur .
Les solutions sur l'intervalle sont .
Etape 2 : on résout : puis on va utiliser le cercle trigonométrique.
.

