Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie - Exercice 1
1 h 30 min
125
Le plan est rapporté à un repère orthonormal . On considère la fonction , définie sur l’intervalle par : . On note sa courbe représentative.
Question 1
Résoudre dans l’équation .
Correction
Soit un réel strictement positif.
équivaut successivement à :
On va effectuer un changement de variable. On pose
Il en résulte que .
On utilise le discriminant
Il en résulte donc que l'équation n'a pas de solutions sur .
équivaut successivement à :
On va effectuer un changement de variable. On pose
Il en résulte que .
On utilise le discriminant
. Il n'y a donc pas de racines réelles.
Il en résulte donc que l'équation n'a pas de solutions sur .
Question 2
Déterminer la limite de en .
Correction
Soit
Il en résulte que la courbe représentative de la fonction admet une asymptote verticale d'équation .
Il en résulte que la courbe représentative de la fonction admet une asymptote verticale d'équation .
Question 3
Déterminer la limite en .
Correction
Soit
Nous rencontrons une forme indéterminée.
Pour relever cette indétermination, nous allons transformer en factorisant l'expression de . En effet :
équivaut successivement à :
. On factorise par . Il vient :
Nous rencontrons une forme indéterminée.
Pour relever cette indétermination, nous allons transformer en factorisant l'expression de . En effet :
équivaut successivement à :
. On factorise par . Il vient :
Question 4
Calculer
Correction
est dérivable sur . Pour faciliter le calcul de la dérivée de , on introduit une fonction dérivable sur et définie par
On reconnaît ici où et . Ainsi .
Il en résulte que :
Finalement :
Maintenant nous allons pouvoir calculer la dérivée de .
Il vient que :
que l'on peut aussi écrire :
Ainsi :
Il en résulte que :
Finalement :
Maintenant nous allons pouvoir calculer la dérivée de .
Il vient que :
que l'on peut aussi écrire :
Ainsi :
Question 5
Étudier le sens de variation de et dresser son tableau de variation.
Correction
Nous savons que
Pour tout réel appartenant à l'intervalle , on vérifie aisément que . Ainsi le signe de dépend de .
équivaut successivement à :
car
Cela signifie que l'on mettra le signe pour le signe de dès que . On en déduit le tableau de variation de .
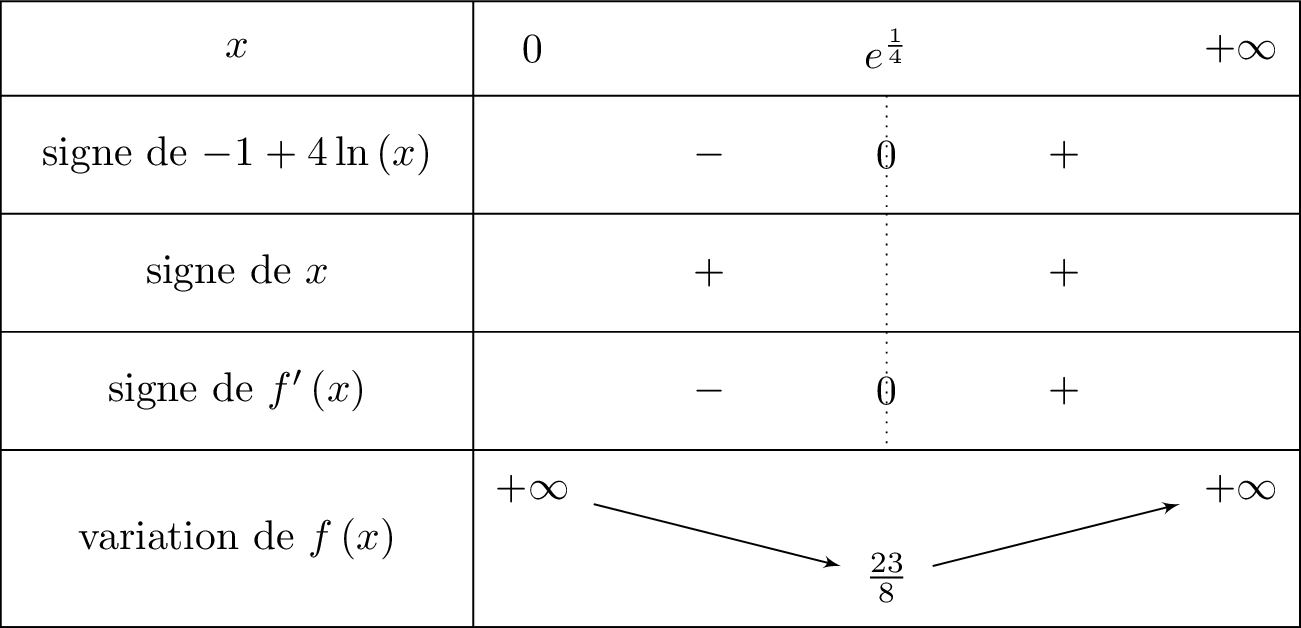 . Or .
. Or .
d'où :
Pour tout réel appartenant à l'intervalle , on vérifie aisément que . Ainsi le signe de dépend de .
équivaut successivement à :
car
Cela signifie que l'on mettra le signe pour le signe de dès que . On en déduit le tableau de variation de .

d'où :
Question 6
Déterminer une équation de la tangente à la courbe au point d’abscisse .
Correction
L'équation de la tangente au point d'abscisse s'écrit .
Ici , ce qui donne : 1ère étape : calculer
. Or .
d'où :
2ème étape : calculer
. Or .
3ème étape : on remplace les valeurs de et de dans la formule de l'équation de tangente.
On sait que :
Ainsi l'équation de la tangente à la courbe au point d'abscisse est alors .
Question 7
On se propose d’étudier la position de la courbe par rapport à la droite .
Pour cela, on considère la fonction , définie sur par :
Pour cela, on considère la fonction , définie sur par :
Montrer que .
Correction
est dérivable sur .
Nous savons que :
Il vient alors que :
. Or d'après la question , nous savons que :
Il en résulte donc que :
Nous savons que :
Il vient alors que :
. Or d'après la question , nous savons que :
Il en résulte donc que :
Question 8
Calculer .
Correction
est dérivable sur .
Ici on reconnaît la forme : avec ; et .
Ainsi : ; et .
Il vient alors que :
Ici on reconnaît la forme : avec ; et .
Ainsi : ; et .
Il vient alors que :
Question 9
Étudier le sens de variation de sur .
Correction
Nous savons que : .
Pour tout réel appartenant à l'intervalle , on vérifie aisément que . Ainsi le signe de dépend de .
équivaut successivement à :
car
Cela signifie que l'on mettra le signe pour le signe de dès que . On en déduit le tableau de variation de .
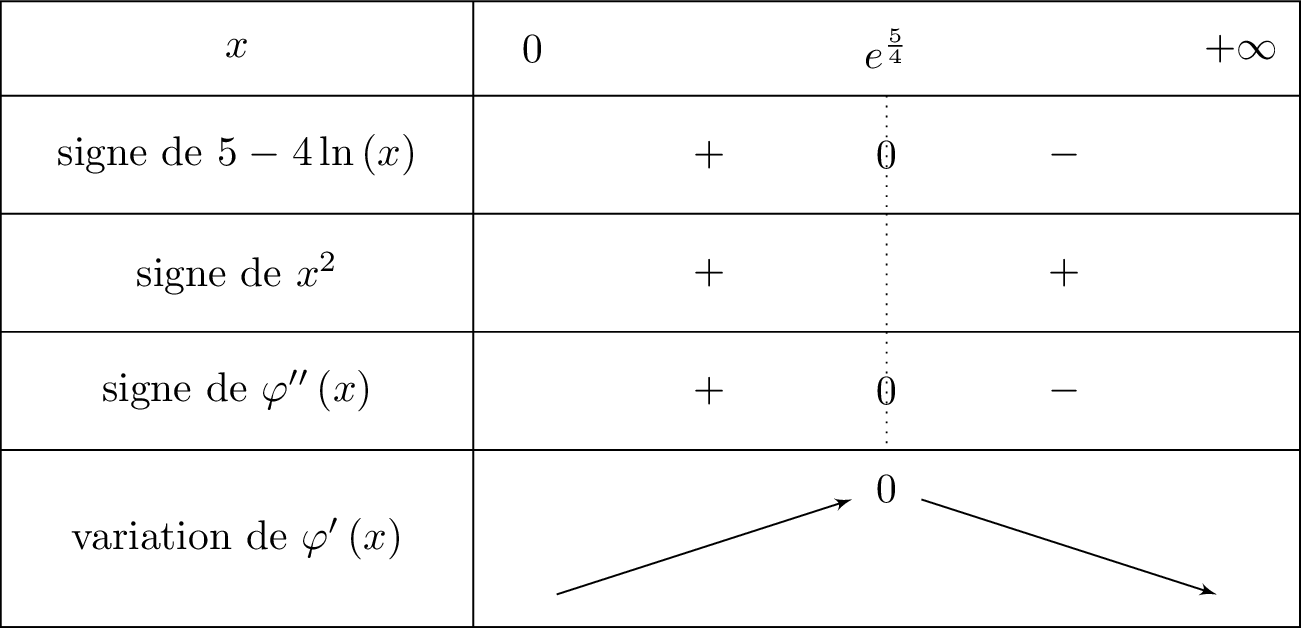 . Or .
. Or .
Pour tout réel appartenant à l'intervalle , on vérifie aisément que . Ainsi le signe de dépend de .
équivaut successivement à :
car
Cela signifie que l'on mettra le signe pour le signe de dès que . On en déduit le tableau de variation de .

Question 10
En déduire le signe de sur .
Correction
D'après la question précédente, nous avons déterminé le tableau de variation de .
 La fonction admet en un maximum qui vaut . La fonction est négative ou nulle sur l'intervalle .
La fonction admet en un maximum qui vaut . La fonction est négative ou nulle sur l'intervalle .
Il en résulte donc que , pour tout réel , . Nous pouvons donc déterminer le tableau de variation de la fonction .
Ainsi :
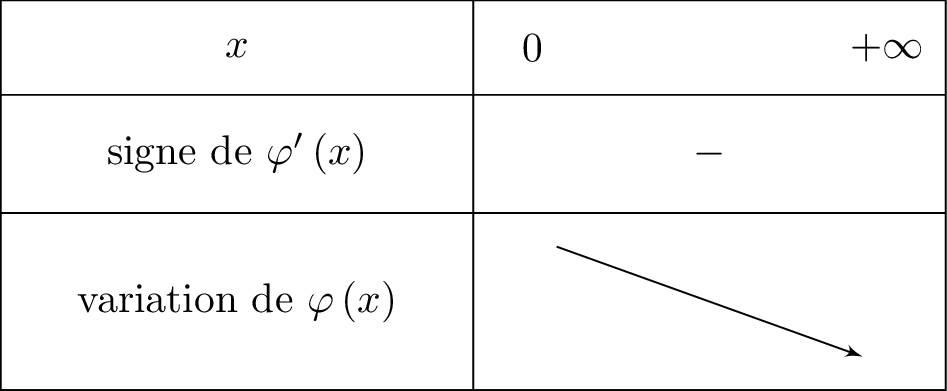

Il en résulte donc que , pour tout réel , . Nous pouvons donc déterminer le tableau de variation de la fonction .
Ainsi :

Question 11
Calculer et en déduire le signe de sur l'intervalle .
Correction
. D'après la question , nous avons vu que : . Ainsi :
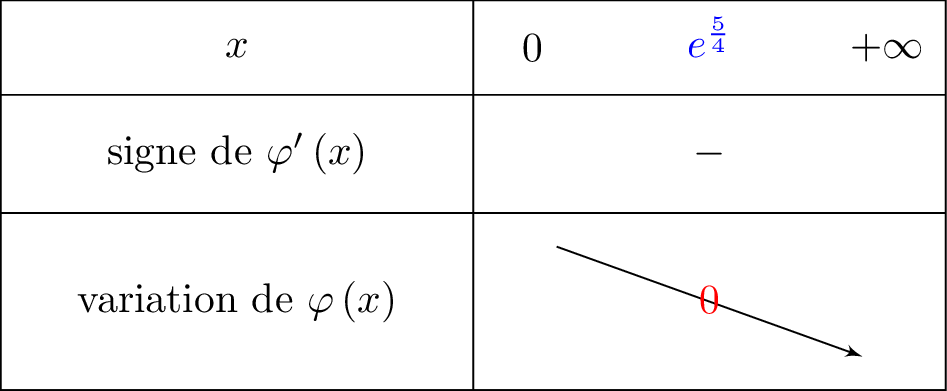 Sur , la fonction est continue et strictement décroissante et
Sur , la fonction est continue et strictement décroissante et
Donc pour tout et pour tout
On résume cela dans un tableau le signe de :
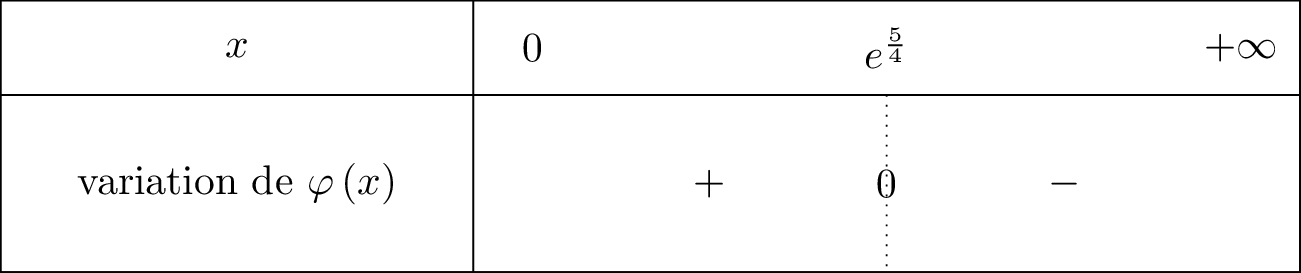
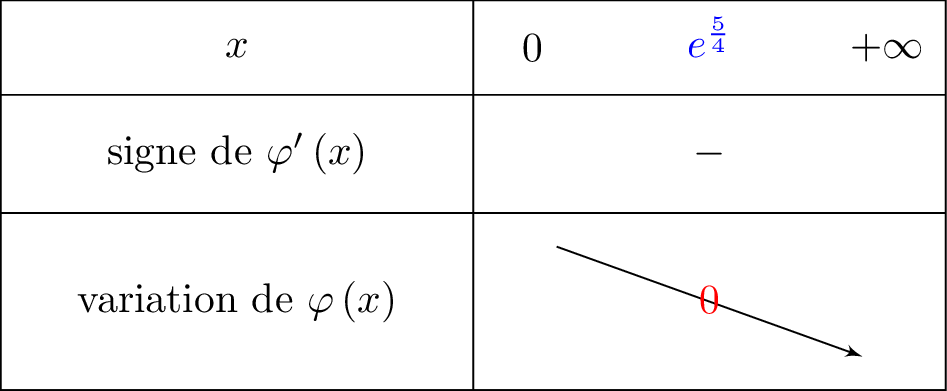
Donc pour tout et pour tout
On résume cela dans un tableau le signe de :

Question 12
En déduire la position de la courbe par rapport à la droite .
Correction
La position relative entre deux courbes étudie les intervalles sur lesquelles une des courbes est supérieure à l'autre.
Pour étudier la position relative entre et , il faut étudier le signe de .
Nous savons que Pour étudier la position relative entre et , il faut étudier le signe de .
- Si sur un intervalle alors la courbe représentative de est au-dessus de sur .
- Si sur un intervalle alors la courbe représentative de est en dessous de sur .
- Si en un point de l'intervalle alors la courbe représentative de et ont un point en commun en .

- Si alors soit . Il en résulte que la courbe est au-dessus de la tangente .
- Si alors soit . Il en résulte que la courbe est en dessous de la tangente .
- Si alors soit alors la courbe et la tangente sont sécantes.