Epreuve d'enseignement de spécialité Centres étrangers 6 juin 2024 . Exercice 2. Fonction exponentielle & convexité - Exercice 1

35 min
55
On considère la fonction ff définie sur l'intervalle ]−∞;1[\left]-\infty ; 1\right[ par f(x)=exx−1f(x)=\frac{\mathrm{e}^x}{x-1} .
On admet que la fonction ff est dérivable sur l'intervalle ]−∞;1[\left]-\infty ; 1\right[. On appelle C\mathscr{C} sa courbe représentative dans un repère.
Question 1

Déterminer la limite de la fonction ff en 11 . En déduire une interprétation graphique.

Correction
lim⁡x→1−ex=elim⁡x→1−x−1=0−}\left. \begin{array}{ccc} {\mathop{\lim }\limits_{x\to 1^{-}} \mathrm{e}^x} & {=} & {\mathrm{e}} \\ {\lim\limits_{x\to 1^{-}} x-1} & {=} & {0^{-} } \end{array}\right\} par quotient :\text{\red{par quotient :}}
lim⁡x→1−exx−1=−∞{\mathop{\lim }\limits_{x\to 1^{-}}} \frac{\mathrm{e}^x}{x-1}=-\infty
Si lim⁡x→nombref(x)=+∞\lim\limits_{x\to \text{nombre}} f(x) =+\infty alors la fonction ff admet une asymptote verticale d'équation x=nombrex=\text{nombre}
Si lim⁡x→nombref(x)=−∞\lim\limits_{x\to \text{nombre}} f(x) =-\infty alors la fonction ff admet une asymptote verticale d'équation x=nombrex=\text{nombre}
On en déduit que la courbe C\mathscr{C} admet une asymptote verticale, d'équation x=1x=1.
Question 2

Déterminer la limite de la fonction ff en −∞-\infty .

Correction
lim⁡x→−∞ex=0lim⁡x→−∞x−1=−∞}\left. \begin{array}{ccc} {\lim\limits_{x\to -\infty } \mathrm{e}^x} & {=} & {0} \\ {\lim\limits_{x\to -\infty } x-1} & {=} & {-\infty } \end{array}\right\} par quotient :\text{\red{par quotient :}}
lim⁡x→−∞exx−1=0{\mathop{\lim }\limits_{x\to -\infty }} \frac{\mathrm{e}^x}{x-1}=0
Question 3

Montrer que pour tout réel xx de l'intervalle ]−∞;1[\left]-\infty ; 1\right[, on a f′(x)=(x−2)ex(x−1)2f^{\prime}(x)=\frac{(x-2) \mathrm{e}^x}{(x-1)^2} .

Correction
ff est dérivable sur ]−∞;1[]-\infty ; 1[
    Deˊriveˊe du quotient\text{\purple{Dérivée du quotient}}
On considère deux fonctions uu et vv, dérivables sur un intervalle II alors
(uv)′=u′v−uv′v2\left(\frac{u}{v} \right)^{'} =\frac{u'v-uv'}{v^{2} }
On reconnaît la forme (uv)′=u′v−uv′v2\color{red}\boxed{\left(\frac{u}{v} \right)^{'} =\frac{u'v-uv'}{v^{2} }} avec u(x)=exu\left(x\right)=\mathrm{e}^x et v(x)=x−1v\left(x\right)=x-1
Ainsi : u′(x)=exu'\left(x\right)=\mathrm{e}^x et v′(x)=1v'\left(x\right)=1.
Il vient alors que :
f′(x)=ex×(x−1)−ex×1(x−1)2 f^{\prime}(x) =\frac{{\color{blue}{\mathrm{e}^x}} \times(x-1)-{\color{blue}{\mathrm{e}^x}} \times 1}{(x-1)^2} . On factorise maintenant par ex{\color{blue}{\mathrm{e}^x}}
f′(x)=ex×(x−1−1)(x−1)2 f^{\prime}(x)=\frac{{\color{blue}{\mathrm{e}^x}} \times(x-1-1)}{(x-1)^2}
Ainsi :
f′(x)=(x−2)ex(x−1)2 f^{\prime}(x)=\frac{(x-2) \mathrm{e}^x}{(x-1)^2}
Question 4

Dresser, en justifiant, le tableau de variations de la fonction ff sur l'intervalle ]−∞;1[\left]-\infty ; 1\right[.

Correction
D'après la question précédente, nous savons que pour tout x∈]−∞;1[x\in \left]-\infty ; 1\right[ on a f′(x)=(x−2)ex(x−1)2 f^{\prime}(x)=\frac{(x-2) \mathrm{e}^x}{(x-1)^2}.
Pour tout réel x∈]−∞;1[x\in \left]-\infty ; 1\right[, on vérifie aisément que (x−1)2>0(x-1)^2>0 et ex>0\mathrm{e}^x>0.
Le signe de f′f' dépend alors du numérateur x−2x-2 .
x−2≥0x-2\ge 0
x≥−2x\ge -2
Cela signifie que l'on va mettre le signe ++ dans la ligne de x−2x-2 lorsque xx sera supérieur ou égale à −2-2.
Il en résulte donc que :
  • si x∈]−∞;−2]x\in\left]-\infty;-2\right] alors f′(x)≤0f'\left(x\right)\le0 et donc ff est décroissante sur cet intervalle.
  • si x∈[−2;1[x\in\left[-2;1\right[ alors f′(x)≥0f'\left(x\right)\ge0 et donc ff est croissante sur cet intervalle.
Nous traduisons toutes ces informations dans le tableau de variation ci-dessous :
Question 5
On admet que pour tout réel xx de l'intervalle ]−∞;1[\left]-\infty ; 1\right[, on a f′′(x)=(x2−4x+5)ex(x−1)3f^{\prime \prime}(x)=\frac{\left(x^2-4 x+5\right) \mathrm{e}^x}{(x-1)^3} .

Étudier la convexité de la fonction ff sur l'intervalle ]−∞;1[\left]-\infty ; 1\right[.

Correction
  • Lorsque f′′(x)≥0f''\left(x\right)\ge 0 sur un intervalle [a,b]\left[a,b\right] alors ff est convexe.
  • Lorsque f′′(x)≤0f''\left(x\right)\le 0 sur un intervalle [a,b]\left[a,b\right] alors ff est concave.
On admet que pour tout réel xx de l'intervalle ]−∞;1[\left]-\infty ; 1\right[, on a f′′(x)=(x2−4x+5)ex(x−1)3f^{\prime \prime}(x)=\frac{\left(x^2-4 x+5\right) \mathrm{e}^x}{(x-1)^3} .
Pour tout réel x∈]−∞;1[x\in \left]-\infty ; 1\right[, on vérifie aisément que (x−1)3<0(x-1)^3<0 car sur cet intervalle x−1<0x-1<0.
De plus, ex>0\mathrm{e}^x>0 . Il nous faut étudier le signe de x2−4x+5x^2-4 x+5 sur l'intervalle ]−∞;1[\left]-\infty ; 1\right[ .
Δ=(−4)2−4×1×5=−4\Delta=(-4)^2-4 \times 1 \times 5=-4.
Comme Δ<0\Delta <0 alors l'équation n'admet pas de racines réelles.
Comme a>0a>0, la parabole est tourné vers le haut c'est-à-dire que x2−4x+5x^2-4 x+5 est du signe de aa et ne passe jamais par l'axe des abscisses.
Il en résulte donc que :
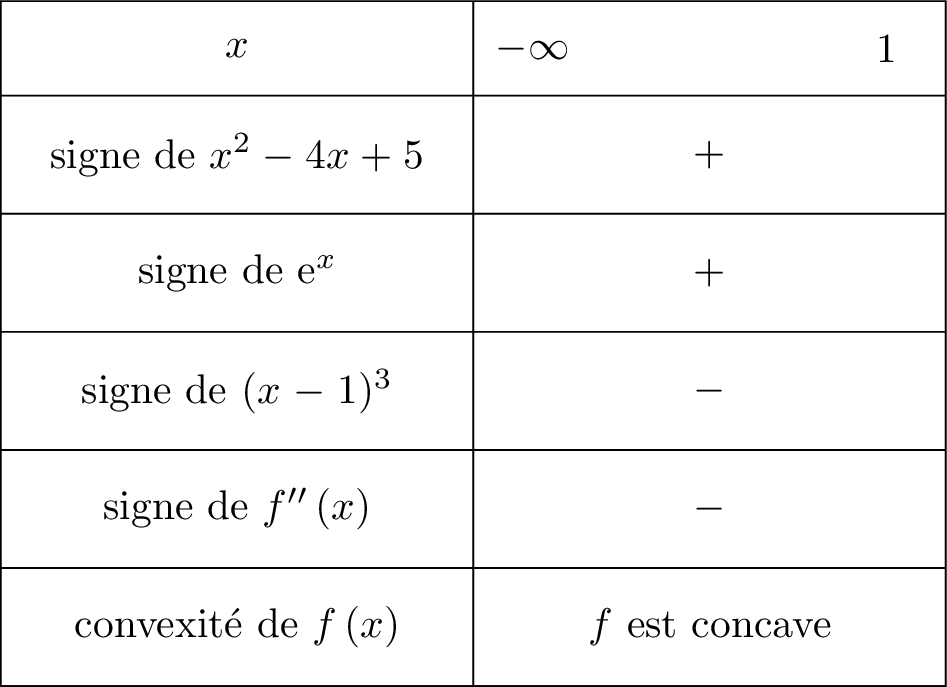
Question 6

Déterminer l'équation réduite de la tangente TT à la courbe C\mathscr{C} au point d'abscisse 00 .

Correction
Comme f(x)=exx−1f(x)=\frac{\mathrm{e}^x}{x-1} alors f(0)=e00−1=−1f(0)=\frac{\mathrm{e}^0}{0-1}=-1
Comme f′(x)=(x−2)ex(x−1)2 f^{\prime}(x)=\frac{(x-2) \mathrm{e}^x}{(x-1)^2} alors f′(0)=(0−2)e0(0−1)2=−2 f^{\prime}(0)=\frac{(0-2) \mathrm{e}^0}{(0-1)^2}=-2
L'équation de la tangente au point d'abscisse aa s'écrit y=f′(a)(x−a)+f(a)y=f'\left(a\right)\left(x-a\right)+f\left(a\right).
Ici a=0a=0, ce qui donne, y=f′(0)(x−0)+f(0)y=f'\left(0\right)\left(x-0\right)+f\left(0\right).
D'où :
y=−2(x−0)−1y=-2\left(x-0\right)-1.
L'équation réduite de la tangente TT à la courbe C\mathscr{C} au point d'abscisse 00 est alors :
y=−2x−1y=-2x-1
Question 7

En déduire que, pour tout réel xx de l'intervalle ]−∞;1[\left]-\infty ; 1\right[, on a : ex⩾(−2x−1)(x−1)\mathrm{e}^x \geqslant(-2 x-1)(x-1) .

Correction

    Les deux définitions ci-dessous sont équivalentes :
  • ff est une fonction concave\red{\text{concave}} sur un intervalle II si sa courbe représentative Cf\mathscr{C_f} est située entièrement en-dessous de chacune de ses tangentes .\red{\text{en-dessous de chacune de ses tangentes .}}
  • ff est une fonction concave\red{\text{concave}} sur un intervalle II si chacune de ses tangentes sont au-dessus\red{\text{au-dessus}} de la courbe représentative Cf\mathscr{C_f} .
    • D'après la question 55, la fonction ff est concave sur l'intervalle ]−∞;1[\left]-\infty ; 1\right[ . Sa courbe est alors située en dessous de chacunes de ces tangentes. En particulier, elle est en dessous de la tangente au point d'abscisse 00.
    Ainsi pour tout réel x∈]−∞;1[x\in \left]-\infty ; 1\right[, on a :
    f(x)≤−2x−1f\left(x\right)\le -2x-1
    exx−1≤−2x−1\frac{\mathrm{e}^x}{x-1}\le -2x-1
    Sur l'intervalle ]−∞;1[\left]-\infty ; 1\right[ nous savons que x−1<0x-1<0 .
    Nous allons multiplier chaque membre par x−1x-1 et donc nous allons changer le sens de l'inégalité.
    exx−1×(x−1)≥(−2x−1)×(x−1)\frac{\mathrm{e}^x}{x-1}\times(x-1)\ge(-2 x-1)\times(x-1)
    Finalement, pour tout réel xx de l'intervalle ]−∞;1[\left]-\infty ; 1\right[, on a :
    ex⩾(−2x−1)(x−1)\mathrm{e}^x \geqslant(-2 x-1)(x-1)
    Question 8

    Justifier que l'équation f(x)=−2f(x)=-2 admet une unique solution α\alpha sur l'intervalle ]−∞;1[\left]-\infty ; 1\right[.

    Correction
  • Sur ]−∞;1[\left]-\infty ; 1\right[ , la fonction ff est continue et strictement décroissante.
    De plus, lim⁡x→−∞f(x)=0\lim _{x \rightarrow -\infty}{f(x)} = 0 et lim⁡x→1−f(x)=−∞{\mathop{\lim }\limits_{x\to 1^{-}}} f(x)=-\infty
    Or −2∈]−∞;1[-2 \in \left]-\infty;1\right[ , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution α\alpha appartenant à ]−∞;1[\left]-\infty;1\right[ tel que f(x)=−2f(x) = -2.
    • Question 9

    À l'aide de la calculatrice, déterminer un encadrement de α\alpha d'amplitude 10−210^{-2}.

    Correction
    À l'aide de la calculatrice, on a :
  • f(0,31)≈−1,98>−2f(0,31) \approx-1,98>-2
  • f(0,32)≈−2,03<−2f(0,32) \approx-2,03<-2
    • Un encadrement de α\alpha d'amplitude 10−210^{-2} est 0,31<α<0,320,31<\alpha<0,32.

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.