Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Tchat avec un prof
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Epreuve d'enseignement de spécialité ASIE 8 juin 2021 sujet 2 Exercice 3 : Dénombrement et Loi Binomiale - Exercice 1
30 min
50
Une société de jeu en ligne propose une nouvelle application pour smartphone nommée « Tickets cœurs! ».
Chaque participant génère sur son smartphone un ticket comportant une grille de taille sur laquelle sont placés trois cœurs répartis au hasard, comme par exemple ci-dessous.
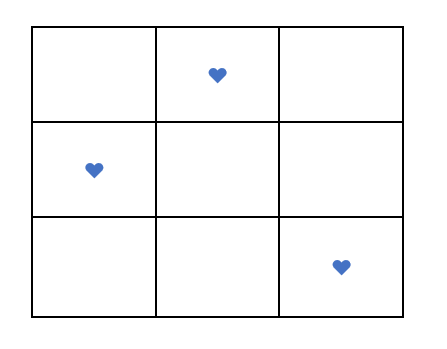 Le ticket est gagnant si les trois cœurs sont positionnés côte à côte sur une même ligne, sur une même colonne ou sur une même diagonale.
Le ticket est gagnant si les trois cœurs sont positionnés côte à côte sur une même ligne, sur une même colonne ou sur une même diagonale.
Chaque participant génère sur son smartphone un ticket comportant une grille de taille sur laquelle sont placés trois cœurs répartis au hasard, comme par exemple ci-dessous.

Question 1
Justifier qu’il y a exactement façons différentes de positionner les trois cœurs sur une grille
Correction
Un ticket comporte une grille de taille sur laquelle sont placés trois cœurs répartis au hasard. Il s'agit d'une combinaison de éléments dans un ensemble de .
Il en résulte donc que le nombre de tirages possibles est égale à :
Ainsi :
Il y a, donc, exactement façons différentes de positionner les trois cœurs sur une grille
Dans une ,
Question 2
Montrer que la probabilité qu’un ticket soit gagnant est égale à .
Correction
Nous allons noter l'évènement la probabilité qu’un ticket soit gagnant.
Il y a lignes, colonnes et diagonales donc combinaisons gagnantes.
La probabilité qu’un ticket soit gagnant est égale à :
Ainsi :
Il y a lignes, colonnes et diagonales donc combinaisons gagnantes.
La probabilité qu’un ticket soit gagnant est égale à :
Ainsi :
Question 3
Lorsqu’un joueur génère un ticket, la société prélève euro sur son compte en banque.
Si le ticket est gagnant, la société verse alors au joueur euros . Le jeu est-il favorable au joueur ?
Si le ticket est gagnant, la société verse alors au joueur euros . Le jeu est-il favorable au joueur ?
Correction
D'après la question précédente, nous avons vu que la probabilité qu’un ticket soit gagnant est égale à .
Lorsqu’un joueur génère un ticket, la société prélève euro sur son compte en banque.
Si le ticket est gagnant, la société verse alors au joueur euros .
On note la variable aléatoire égale au gain algébrique d’un joueur (c’est-à-dire la somme remportée à laquelle on soustrait la somme prélevée sur son compte).
La variable aléatoire prend les valeurs suivantes : .
On a donc :
et car
La loi de probabilité de est donnée ci-dessous :
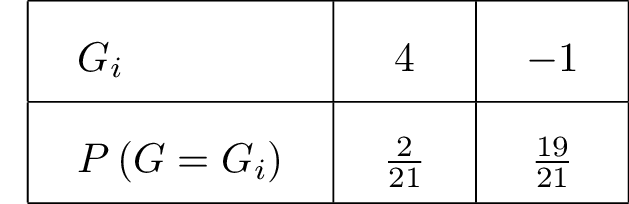 Dans un premier temps, nous allons calculer l'espérance de la variable aléatoire .
Dans un premier temps, nous allons calculer l'espérance de la variable aléatoire .
Ainsi : ou encore
En moyenne sur un grand nombre de parties un joueur perd centimes d’euro par partie. Le jeu est donc défavorable au joueur.
Lorsqu’un joueur génère un ticket, la société prélève euro sur son compte en banque.
Si le ticket est gagnant, la société verse alors au joueur euros .
On note la variable aléatoire égale au gain algébrique d’un joueur (c’est-à-dire la somme remportée à laquelle on soustrait la somme prélevée sur son compte).
La variable aléatoire prend les valeurs suivantes : .
On a donc :
et car
La loi de probabilité de est donnée ci-dessous :
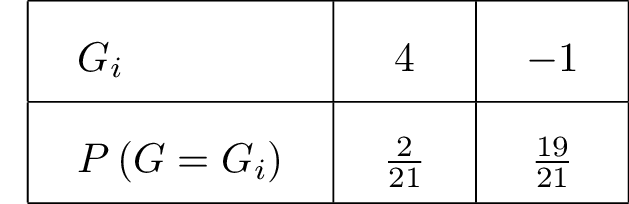
- On appelle l’espérance mathématique de la variable , la quantité notée définie par :
Ainsi :
En moyenne sur un grand nombre de parties un joueur perd centimes d’euro par partie. Le jeu est donc défavorable au joueur.
- Pour que le jeu soit favorable au joueur, il faut que l'espérance soit strictement positive.
- Pour que le jeu soit défavorable au joueur, il faut que l'espérance soit strictement positive.
- Si l'espérance est nulle, on dit que le jeu est équitable.
Question 4
Un joueur décide de générer tickets sur cette application. On suppose que les générations des tickets sont indépendantes entre elles.
Donner la loi de probabilité de la variable aléatoire qui compte le nombre de tickets gagnants parmi les tickets générés.
Donner la loi de probabilité de la variable aléatoire qui compte le nombre de tickets gagnants parmi les tickets générés.
Correction
On considère l'expérience ci-dessous
On appelle « le ticket est gagnant » avec la probabilité On appelle « le ticket est perdant » avec la probabilité On répète fois de suite cette expérience de Bernoulli de .
On est donc en présence
est la variable aléatoire qui associe le nombre de tickets gagnants.
suit la loi binomiale de paramètre et
On note alors suit la loi binomiale
On est donc en présence
est la variable aléatoire qui associe le nombre de tickets gagnants.
suit la loi binomiale de paramètre et
On note alors suit la loi binomiale
Question 5
Calculer la probabilité, arrondie à , de l’évènement .
Correction
suit la loi binomiale
Il nous faut calculer
Avec la formule du cours
En utilisant les fonctionnalités de la calculatrice
on tape pour
(tu peux regarder la vidéo "Utiliser la loi binomiale avec une Texas" pour plus de détails)
2nd - DISTR -- puis choisir BinomFdp(valeur de n, valeur de p, valeur de k) c'est-à-dire ici BinomFdp(20, , 5) puis taper sur enter et on obtient :
Pour certaine version de Texas, on aura BinomPdf au lieu de BinomFdp
on tape pour :
(tu peux regarder la vidéo "Utiliser la loi binomiale avec une Casio" pour plus de détails)
Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR.
On remplit le tableau de la manière qui suit :
puis taper sur EXE et on obtient :
Il nous faut calculer
Avec la formule du cours
Soit une variable aléatoire suivant la loi binomiale alors, pour tout entier compris entre et , on a :
Ainsi : En utilisant les fonctionnalités de la calculatrice
on tape pour
(tu peux regarder la vidéo "Utiliser la loi binomiale avec une Texas" pour plus de détails)
2nd - DISTR -- puis choisir BinomFdp(valeur de n, valeur de p, valeur de k) c'est-à-dire ici BinomFdp(20, , 5) puis taper sur enter et on obtient :
arrondi à près.
Pour certaine version de Texas, on aura BinomPdf au lieu de BinomFdp
on tape pour :
(tu peux regarder la vidéo "Utiliser la loi binomiale avec une Casio" pour plus de détails)
Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR.
On remplit le tableau de la manière qui suit :
D.P. Binomiale
Data Variable
: valeur de
Numtrial : valeur de
: valeur de
Data Variable
: valeur de
Numtrial : valeur de
: valeur de
puis taper sur EXE et on obtient :
arrondi à près.
Question 6
Calculer la probabilité, arrondie à , de l’évènement et interpréter le résultat dans le contexte de l’exercice.
Correction
On doit calculer : .
Or :
Finalement :
Or :
Soit une variable aléatoire suivant la loi binomiale alors, pour tout entier compris entre et , on a :
Finalement :
arrondi à près.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.