Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Epreuve d'enseignement de spécialité ASIE 7 juin 2021 sujet 1 Exercice 3 : Dénombrement et Loi Binomiale - Exercice 1
30 min
50
Un sac contient les huit lettres suivantes : A B C D E F G H ( voyelles et consonnes).
Un jeu consiste à tirer simultanément au hasard deux lettres dans ce sac.
On gagne si le tirage est constitué d’une voyelle et d’une consonne.
Un jeu consiste à tirer simultanément au hasard deux lettres dans ce sac.
On gagne si le tirage est constitué d’une voyelle et d’une consonne.
Question 1
Un joueur extrait simultanément deux lettres du sac. Déterminer le nombre de tirages possibles.
Correction
Il en résulte donc que le nombre de tirages possibles est égale à :
Ainsi :
Il y a donc tirages possbiles.
Dans une ,
Question 2
Un joueur extrait simultanément deux lettres du sac. Déterminer la probabilité que le joueur gagne à ce jeu.
Correction
On gagne si le tirage est constitué d’une voyelle et d’une consonne.
Il faut donc prendre voyelle parmi voyennes consonne parmi consonnes. Ce qui nous donne :
Nous allons noter l'évènement la probabilité d’obtenir deux boules de couleurs différentes. Ainsi :
Ainsi :
Il faut donc prendre voyelle parmi voyennes consonne parmi consonnes. Ce qui nous donne :
Nous allons noter l'évènement la probabilité d’obtenir deux boules de couleurs différentes. Ainsi :
Ainsi :
Question 3
Les questions 3 et 4 de cet exercice sont indépendantes.
Pour la suite de l’exercice, on admet que la probabilité que le joueur gagne est égale à .
Pour jouer, le joueur doit payer euros, désignant un entier naturel non nul. Si le joueur gagne, il remporte la somme de euros, sinon il ne remporte rien.
On note la variable aléatoire égale au gain algébrique d’un joueur (c’est-à-dire la somme remportée à laquelle on soustrait la somme payée).
Pour la suite de l’exercice, on admet que la probabilité que le joueur gagne est égale à .
Pour jouer, le joueur doit payer euros, désignant un entier naturel non nul. Si le joueur gagne, il remporte la somme de euros, sinon il ne remporte rien.
On note la variable aléatoire égale au gain algébrique d’un joueur (c’est-à-dire la somme remportée à laquelle on soustrait la somme payée).
Déterminer la loi de probabilité de .
Correction
D'après la question précédente, nous avons vu que la probabilité qu'un joueur gagne est égale à .
Pour jouer, le joueur doit payer euros, désignant un entier naturel non nul. Si le joueur gagne, il remporte la somme de euros, sinon il ne remporte rien.
On note la variable aléatoire égale au gain algébrique d’un joueur (c’est-à-dire la somme remportée à laquelle on soustrait la somme payée).
La variable aléatoire prend les valeurs suivantes : .
On a donc :
et car
La loi de probabilité de est donnée ci-dessous :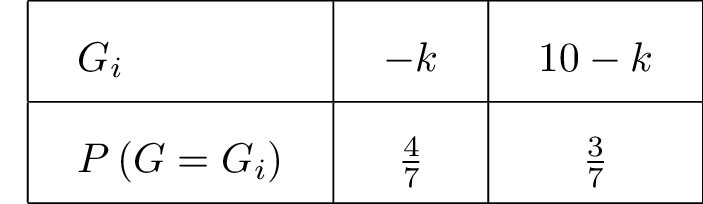
Pour jouer, le joueur doit payer euros, désignant un entier naturel non nul. Si le joueur gagne, il remporte la somme de euros, sinon il ne remporte rien.
On note la variable aléatoire égale au gain algébrique d’un joueur (c’est-à-dire la somme remportée à laquelle on soustrait la somme payée).
La variable aléatoire prend les valeurs suivantes : .
On a donc :
et car
La loi de probabilité de est donnée ci-dessous :
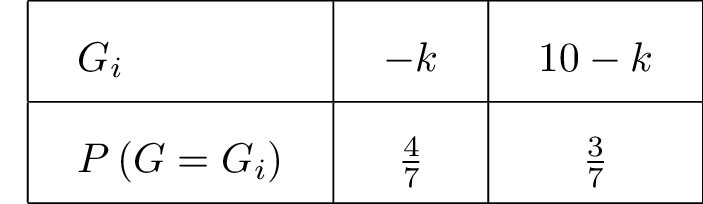
Question 4
Quelle doit être la valeur maximale de la somme payée au départ pour que le jeu reste favorable au joueur ?
Correction
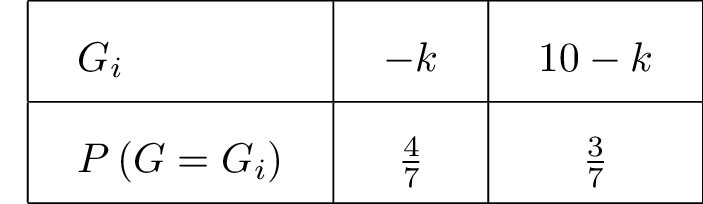
- On appelle l’espérance mathématique de la variable , la quantité notée définie par :
Ainsi :
- Pour que le jeu soit favorable au joueur, il faut que l'espérance soit strictement positive. Car si l'espérance est nulle, on dit que le jeu est équitable.
Soit :
équivaut successivement à :
. Or
On rappelle que pour jouer, le joueur doit payer euros, désignant un entier naturel non nul.
Il en résulte donc que la somme payée au départ pour que le jeu reste favorable au joueur ne doit pas dépasser euros.
Question 5
Dix joueurs font chacun une partie. Les lettres tirées sont remises dans le sac après chaque partie.
On note la variable aléatoire égale au nombre de joueurs gagnants.
On note la variable aléatoire égale au nombre de joueurs gagnants.
Justifier que suit une loi binomiale et donner ses paramètres.
Correction
On considère l'expérience ci-dessous
On appelle « le joueur gagne » avec la probabilité On appelle « le joueur ne gagne pas » avec la probabilité On répète fois de suite cette expérience de Bernoulli de .
On est donc en présence
est la variable aléatoire qui associe le nombre de joueurs gagnants.
suit la loi binomiale de paramètre et
On note alors suit la loi binomiale
On est donc en présence
est la variable aléatoire qui associe le nombre de joueurs gagnants.
suit la loi binomiale de paramètre et
On note alors suit la loi binomiale
Question 6
Calculer la probabilité, arrondie à , qu’il y ait exactement quatre joueurs gagnants.
Correction
suit la loi binomiale
La probabilité qu’il y ait exactement quatre joueurs gagnants se traduit par :
pour on tape :
2nd - DISTR -- puis choisir
BinomFdp(valeur de , valeur de , valeur de ) c'est-à-dire ici BinomFdp(, , ) puis on tape sur enter et on obtient :
Pour certaine version de Texas, on aura BinomPdf au lieu de BinomFdp.
pour on tape :
Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR.
On remplit le tableau de la manière qui suit :
puis on tape sur EXE et on obtient :
Avec une calculatrice Numworks
Choisir Probabilités puis sélectionner Ok puis une nouvelle fois OK puis choisir Binomiale . Entrer les paramètres et .
Puis ensuite choisir le calcul avec l'encadré bleu.
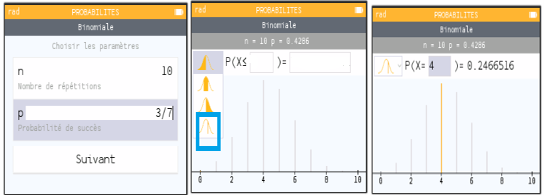
La probabilité qu’il y ait exactement quatre joueurs gagnants se traduit par :
pour on tape :
2nd - DISTR -- puis choisir
BinomFdp(valeur de , valeur de , valeur de ) c'est-à-dire ici BinomFdp(, , ) puis on tape sur enter et on obtient :
arrondi à près.
Pour certaine version de Texas, on aura BinomPdf au lieu de BinomFdp.
pour on tape :
Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR.
On remplit le tableau de la manière qui suit :
D.P. Binomiale
Data Variable
: Valeur de
Numtrial : Valeur de
: Valeur de
Data Variable
: Valeur de
Numtrial : Valeur de
: Valeur de
puis on tape sur EXE et on obtient :
arrondi à près.
Avec une calculatrice Numworks
Choisir Probabilités puis sélectionner Ok puis une nouvelle fois OK puis choisir Binomiale . Entrer les paramètres et .
Puis ensuite choisir le calcul avec l'encadré bleu.

Question 7
Calculer en arrondissant à . Donner une interprétation du résultat obtenu.
Correction
Avec la calculatrice, on obtient :
La probabilité qu’il y ait au moins gagnants sur joueurs est d’environ .
La probabilité qu’il y ait au moins gagnants sur joueurs est d’environ .
Question 8
Déterminer le plus petit entier naturel tel que .
Correction
Pour cette question, il faut procéder une étude à l'aide de la calculatrice.
En effet : et
Ainsi le plus petit entier naturel tel que est alors .
En effet : et
Ainsi le plus petit entier naturel tel que est alors .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.