Qui aura 20 en maths ?
💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Calculs d'intégrales en utilisant les formes composées - Exercice 1
25 min
40
Calculer les intégrales suivantes
Question 1
Correction
Soit : .
On reconnaît la forme .
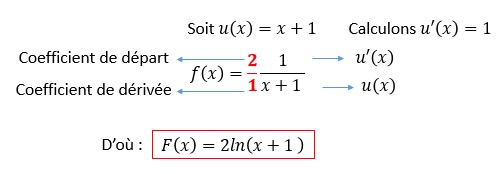 équivaut successivement à
équivaut successivement à
Finalement :
On reconnaît la forme .
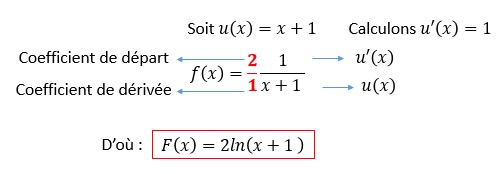
Finalement :
Question 2
Correction
Soit :
On reconnaît la forme
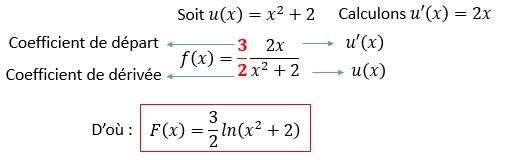
équivaut successivement à.
Finalement :
On reconnaît la forme
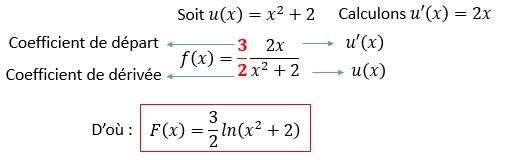
équivaut successivement à.
Finalement :
Question 3
Correction
Soit :
On reconnait la forme

équivaut succesivement à
Finalement :
On reconnait la forme

équivaut succesivement à
Finalement :
Question 4
Correction
Soit :
On reconnaît la forme

équivaut successivement à
Finalement :
On reconnaît la forme

équivaut successivement à
Finalement :
Question 5
Correction
On a : c'est à dire
équivaut successivement à
Finalement :
Question 6
Correction
On a :
équivaut successivement à
Finalement :
Question 7
Correction
Soit :
On reconnait la forme
 équivaut successivement à
équivaut successivement à
Finalement :
On reconnait la forme

Finalement :
Question 8
Correction
Soit :
On reconnait la forme

équivaut successivement à
Finalement :
On reconnait la forme

équivaut successivement à
Finalement :