Calculer l'aire entre deux courbes - Exercice 1

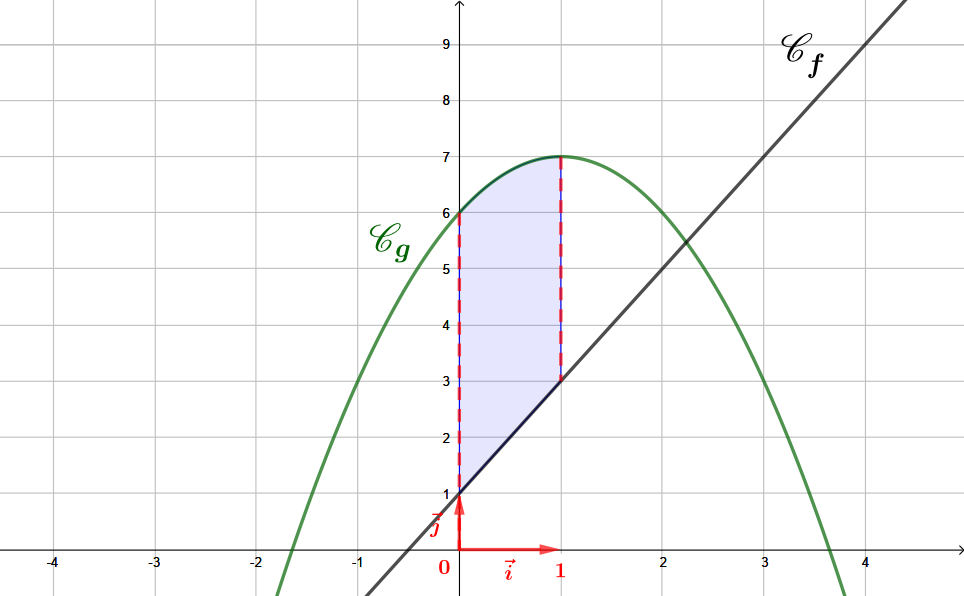
On vérifie facilement sur le graphique ci-dessous que la courbe $$\mathscr{C_g}$$ est au-dessus de la courbe $$\mathscr{C_f}$$ .
Nous avons donc $$g\left(x\right)\ge f\left(x\right)$$ .
Nous allons donc calculer : $$\int _{0}^{1}\left(g\left(x\right)-f\left(x\right)\right) dx$$
Il vient alors que :
$$\int _{0}^{1}\left(g\left(x\right)-f\left(x\right)\right) dx=\int _{0}^{1}\left(-x^{2} +2x+6-\left(2x+1\right)\right) dx$$
$$\int _{0}^{1}\left(g\left(x\right)-f\left(x\right)\right) dx=\int _{0}^{1}\left(-x^{2} +2x+6-2x-1\right) dx$$
$$\int _{0}^{1}\left(g\left(x\right)-f\left(x\right)\right) dx=\int _{0}^{1}\left(-x^{2} +5\right) dx$$
$$\int _{0}^{1}\left(g\left(x\right)-f\left(x\right)\right) dx=\left[-\frac{1}{3} x^{3} +5x\right]_{0}^{1}$$
$$\int _{0}^{1}\left(g\left(x\right)-f\left(x\right)\right) dx=-\frac{1}{3} \times 1^{3} +5\times 1-\left(-\frac{1}{3} \times 0^{3} +5\times 0\right)$$
$$\int _{0}^{1}\left(g\left(x\right)-f\left(x\right)\right) dx=-\frac{1}{3} +5$$
Finalement :
Ci-dessous en violet le domaine (aire) compris entre les courbes représentatives de $$g$$ et $$f$$ sur l'intervalle $$\left[0;1\right]$$ .