Calcul intégral
Baccalauréat Amérique du Nord 22 mai 2024 : Intégration et fonction logarithme népérien - Exercice 1
30 min
50
Soit un réel strictement positif.
On considère la fonction définie sur l'intervalle par
On note sa courbe représentative dans un repère orthonormé.
Soit un réel strictement supérieur à .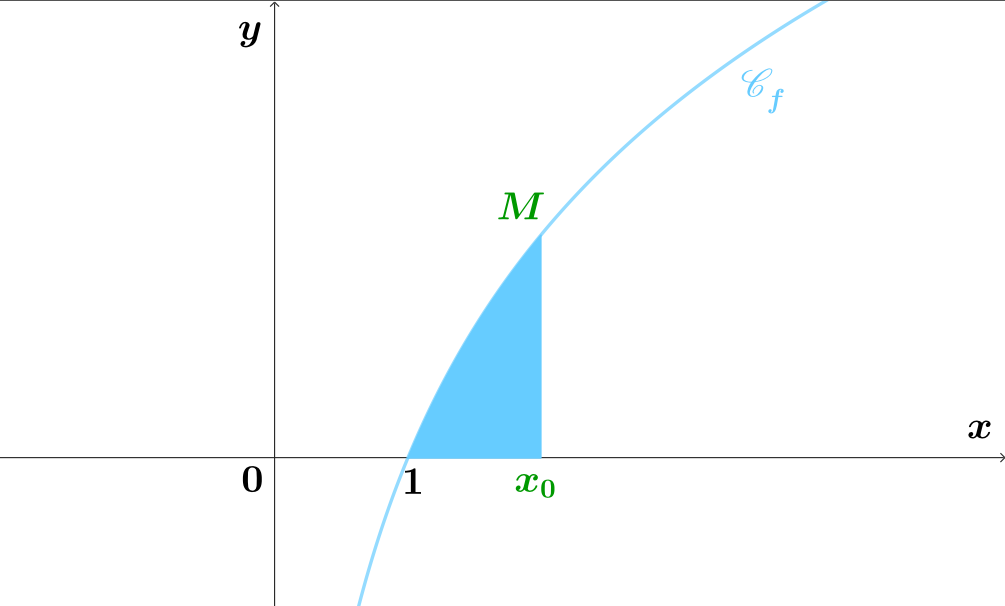
On considère la fonction définie sur l'intervalle par
On note sa courbe représentative dans un repère orthonormé.
Soit un réel strictement supérieur à .

Question 1
Déterminer l'abscisse du point d'intersection de la courbe et de l'axe des abscisses.
Correction
Pour déterminer l'abscisse du point d'intersection de la courbe et de l'axe des abscisses, il nous faut résoudre l'équation . En effet, le point d'intersection de la droite avec l'axe des abscisses a pour ordonnée .
Il vient alors que :
équivaut successivement à :
D'où :
L'abscisse du point d'intersection de la courbe et de l'axe des abscisses est .
Il vient alors que :
équivaut successivement à :
D'où :
L'abscisse du point d'intersection de la courbe et de l'axe des abscisses est .
Question 2
Vérifier que la fonction définie par est une primitive de la fonction sur l'intervalle .
Correction
Il est important d'indiquer que est dérivable sur .
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Ainsi :
Nous avons :
Ainsi :
Finalement :
La fonction définie par est bien une primitive de la fonction sur l'intervalle .
Dans le cas où une primitive est donnée, il vous suffit de dériver et d'obtenir comme résultat .
Autrement dit, il faut que :
On introduit une fonction définie sur par La fonction est dérivable sur .Autrement dit, il faut que :
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Ainsi :
Nous avons :
Ainsi :
Finalement :
La fonction définie par est bien une primitive de la fonction sur l'intervalle .
Question 3
En déduire l'aire du domaine bleuté en fonction de et de .


Correction
une fonction continue et positive sur un intervalle .
En déduire l'aire du domaine bleuté en fonction de et de signifie que l'on recherche l'aire, exprimée en u.a., de la surface délimitée par la courbe représentative de la fonction , l'axe des abscisses et les droites d'équations et .
C'est la définition de l'intégrale de sur .
. On factorise par .
Finalement :
En déduire l'aire du domaine bleuté en fonction de et de signifie que l'on recherche l'aire, exprimée en u.a., de la surface délimitée par la courbe représentative de la fonction , l'axe des abscisses et les droites d'équations et .
C'est la définition de l'intégrale de sur .
. On factorise par .
Finalement :
Question 4
On note la tangente à la courbe au point d'abscisse .
On appelle le point d'intersection de la tangente avec l'axe des ordonnées et le projeté orthogonal de sur l'axe des ordonnées.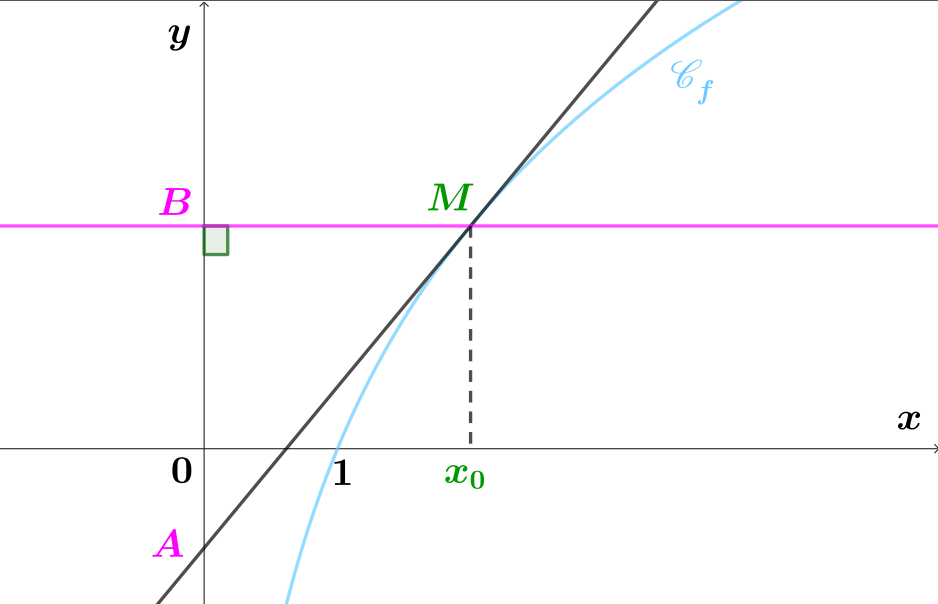
On appelle le point d'intersection de la tangente avec l'axe des ordonnées et le projeté orthogonal de sur l'axe des ordonnées.

Démontrer que la longueur est égale à une constante (c'est-à-dire à un nombre qui ne dépend pas de ) que l'on déterminera.
Correction
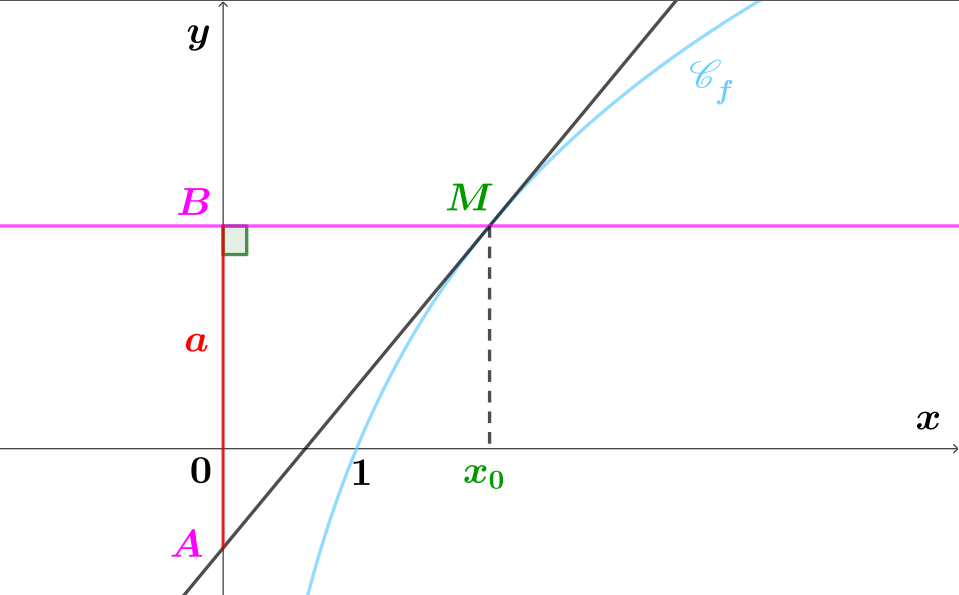
Les coordonnées de sont assez rapides à obtenir. En effet, dans un premier temps nous connaissons les coordonnées du point .
L'abscisse du point est et son ordonnée est car . Ainsi les coordonnées du point sont .
On rappelle que le projeté orthogonal de sur l'axe des ordonnées. Cela signifie que l'abscisse du point vaut car est sur l'axe des abscisses, mais l'ordonnée de est la même que celle du point car le projeté orthogonal de sur l'axe des ordonnées.
Il en résulte que les coordonnées du point sont
.
Maintenant déterminons les coordonnées du point .
On appelle le point d'intersection de la tangente avec l'axe des ordonnées. Cela signifie que l'abscisse du point vaut .
Nous allons dans un premier temps calculer l'équation de la tangente c'est à dire l'équation de la tangente au point d'abscisse .
On rappelle que , est dérivable sur .
On a alors :
.
L'équation de la tangente à la courbe au point d'abscisse est :
D'où :
Le point appartient à l'équation de la tangente à la courbe au point d'abscisse . Il en résulte donc que :
Ainsi les cordonnées du point sont :
.
Nous avons donc et
Nous pouvons donc calculer la distance .
Il s'ensuit que :
. On rappelle que ainsi :
La longueur est égale à une constante .