Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices Types - Exercice 4
20 min
35
Dans un repère orthonormé , on donne les points , , .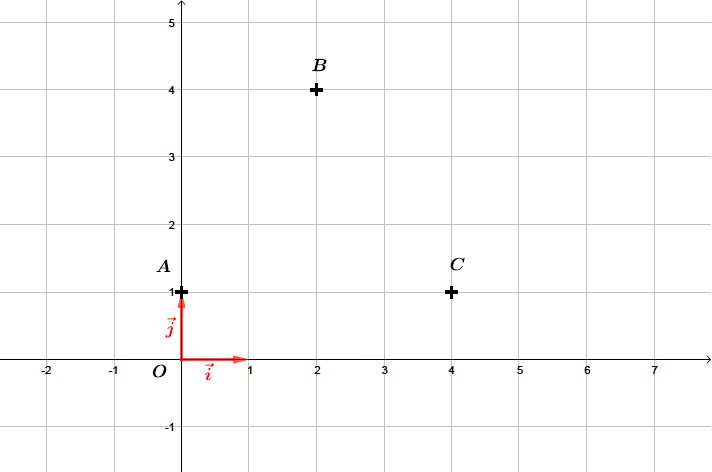

Question 1
On considère le point tel que est un parallélogramme. Traduire cela par une égalité de deux vecteurs.
Correction
Si le point est tel que est un parallélogramme alors les vecteurs opposés sont égaux. De ce fait :
Question 2
Déterminer les coordonnées de pour que soit un parallélogramme.
Correction
Nous savons que .
Commençons par calculer le vecteur .
ainsi d'où : Calculons maintenant le vecteur . Soit les coordonnées du point .
ainsi Comme .
Il en résulte donc que :
On obtient alors deux équations à résoudre. Nous l'écrivons sous forme de système.
Ainsi :
Les coordonnées du point sont alors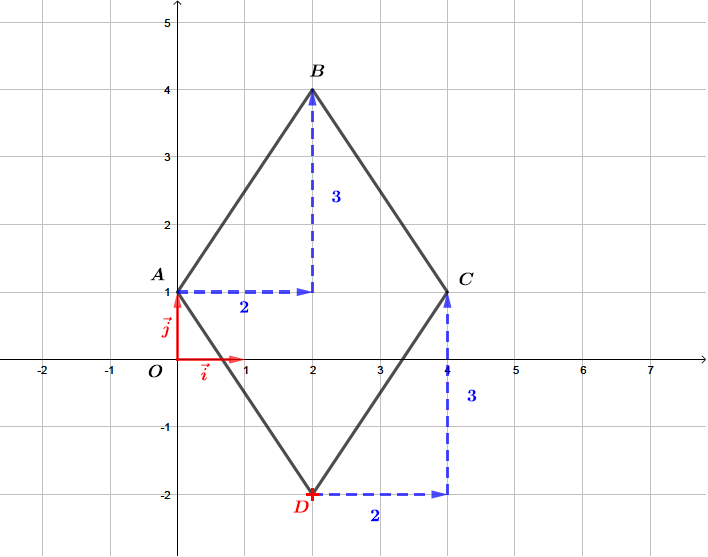
Commençons par calculer le vecteur .
Il en résulte donc que :
On obtient alors deux équations à résoudre. Nous l'écrivons sous forme de système.
Ainsi :
Les coordonnées du point sont alors

Question 3
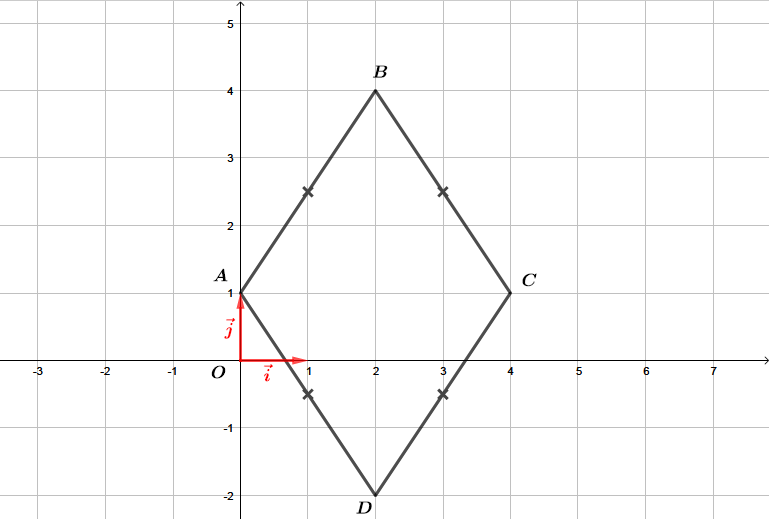
Montrer que est un losange.
Correction
Nous savons que est un parallélogramme.
Il nous suffit de montrer que si deux cotés consécutifs d'un parallélogramme sont égaux alors ce parallélogramme sera alors un losange.
équivaut successivement à :
D'autre part :
équivaut successivement à :
est un parallélogramme avec deux cotés consécutifs égaux. est bien un losange.
Il nous suffit de montrer que si deux cotés consécutifs d'un parallélogramme sont égaux alors ce parallélogramme sera alors un losange.
Soit un repère orthonormal du plan et deux points et . La distance est donnée par la formule :
D'une part : équivaut successivement à :
D'autre part :
équivaut successivement à :
est un parallélogramme avec deux cotés consécutifs égaux. est bien un losange.

Question 4
est-il un carré?
Correction
Nous savons que est un losange. Pour que soit un carré, il faut que les diagonales soient de même mesure. Les diagonales sont ici et .
D'une part :
équivaut successivement à :
D'autre part :
équivaut successivement à :
Les diagonales n'ont pas la même mesure. Le losange n'est donc pas un carré.
D'une part :
équivaut successivement à :
D'autre part :
équivaut successivement à :
Les diagonales n'ont pas la même mesure. Le losange n'est donc pas un carré.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.