Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Comment montrer que deux droites sont paralléles à l'aide de deux vecteurs colinéaires - Exercice 2

5 min
10
Soit (0;i→;j→)\left(0;\overrightarrow{i} ;\overrightarrow{j} \right) un repère du plan. On considère les points A(2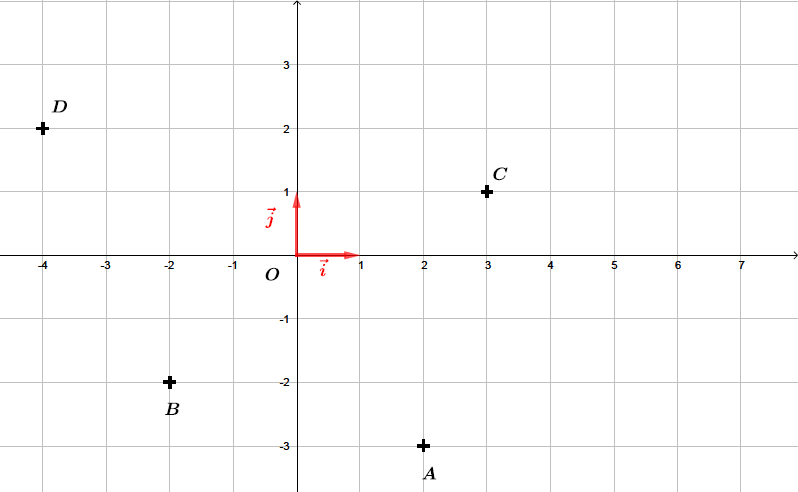;−3)A\left(2;-3\right) ; B(−2;−2)B\left(-2;-2\right) ; C(3;1)C\left(3;1\right) et D(−4;2)D\left(-4;2\right).
Question 1

Les droites (AB)\left(AB\right) et (CD)\left(CD\right) sont-elles parallèles?

Correction
  • Les droites (AB)\left(AB\right) et (CD)\left(CD\right) sont parallèles si, et seulement si les vecteurs AB→\overrightarrow{AB} et CD→\overrightarrow{CD} sont colinéaires.
On commence par calculer les vecteurs AB→\overrightarrow{AB} et CD→\overrightarrow{CD}. Ainsi :
AB→(xB−xAyB−yA)\overrightarrow{AB} \left(\begin{array}{c} {x_{B}-x_{A}} \\ {y_{B}-y_{A}} \end{array}\right) ainsi AB→(−2−2−2−(−3))\overrightarrow{AB} \left(\begin{array}{c} {-2-2} \\ {-2-\left(-3\right)} \end{array}\right) d'où : AB→(−41)\overrightarrow{AB} \left(\begin{array}{c} {-4} \\ {1} \end{array}\right)
CD→(xD−xCyD−yC)\overrightarrow{CD} \left(\begin{array}{c} {x_{D}-x_{C}} \\ {y_{D}-y_{C}} \end{array}\right) ainsi CD→(−4−32−1)\overrightarrow{CD} \left(\begin{array}{c} {-4-3} \\ {2-1} \end{array}\right) d'où : CD→(−71)\overrightarrow{CD} \left(\begin{array}{c} {-7} \\ {1} \end{array}\right)
Maintenant , nous allons vérifier si les vecteurs AB→\overrightarrow{AB} et CD→\overrightarrow{CD} sont colinéaires.
Soit (0;i→;j→)\left(0;\overrightarrow{i} ;\overrightarrow{j} \right) un repère du plan.
  • Deux vecteurs u→(x;y)\overrightarrow{u} \left(x;y\right) et v→(x′;y′)\overrightarrow{v} \left(x';y'\right) sont colinéaires si et seulement si det⁡(u→;v→)=0\det\left(\overrightarrow{u} ;\overrightarrow{v} \right)=0 autrement dit si : xy′−x′y=0xy'-x'y=0.
  • det⁡(u→;v→)=xy′−x′y\det\left(\overrightarrow{u} ;\overrightarrow{v} \right)=xy'-x'y est appelé deˊterminant\text{\color{red}déterminant}.
  • On peut également écrire les vecteurs u→\overrightarrow{u} et v→\overrightarrow{v} sous la forme u→(xy)\overrightarrow{u} \left(\begin{array}{c} {x} \\ {y} \end{array}\right) et v→(x′y′)\overrightarrow{v} \left(\begin{array}{c} {x'} \\ {y'} \end{array}\right).
On a : −4×1−1×(−7)=−4+7=3≠0-4\times 1-1\times\left(-7\right)=-4+7=3\ne0
Nous avons donc
det⁡(u→;v→)≠0\det\left(\overrightarrow{u} ;\overrightarrow{v} \right)\ne0

Les vecteurs AB→\overrightarrow{AB} et CD→\overrightarrow{CD} ne sont pas colinéaires. Donc les droites (AB)\left(AB\right) et (CD)\left(CD\right) ne sont donc pas parallèles.