Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : Lectures graphiques - Exercice 1
20 min
35
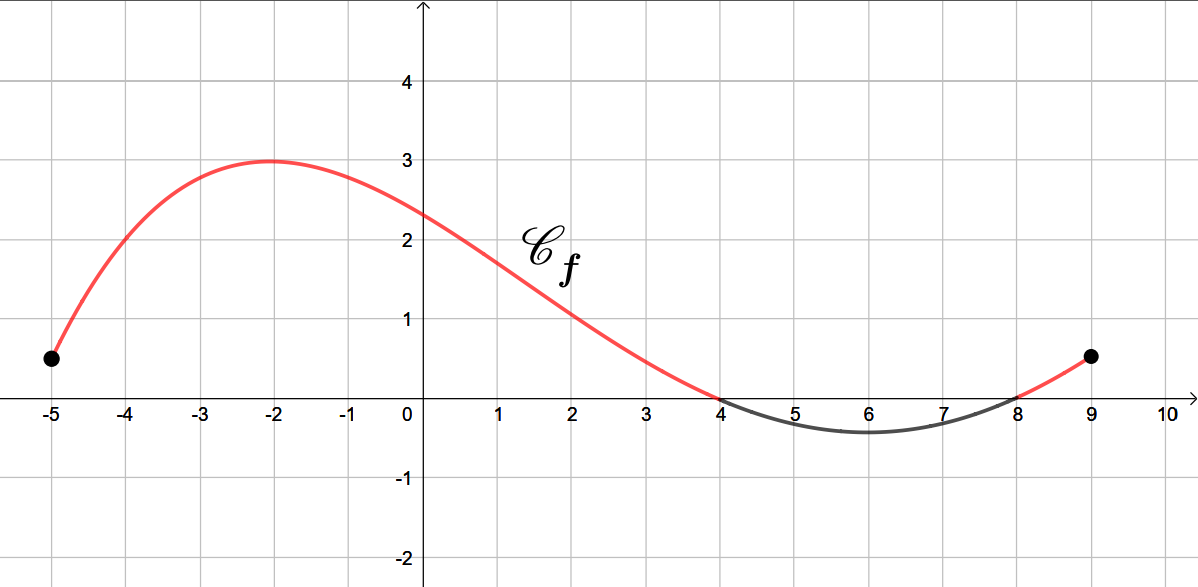
On donne ci-dessous la courbe représentative d'une fonction .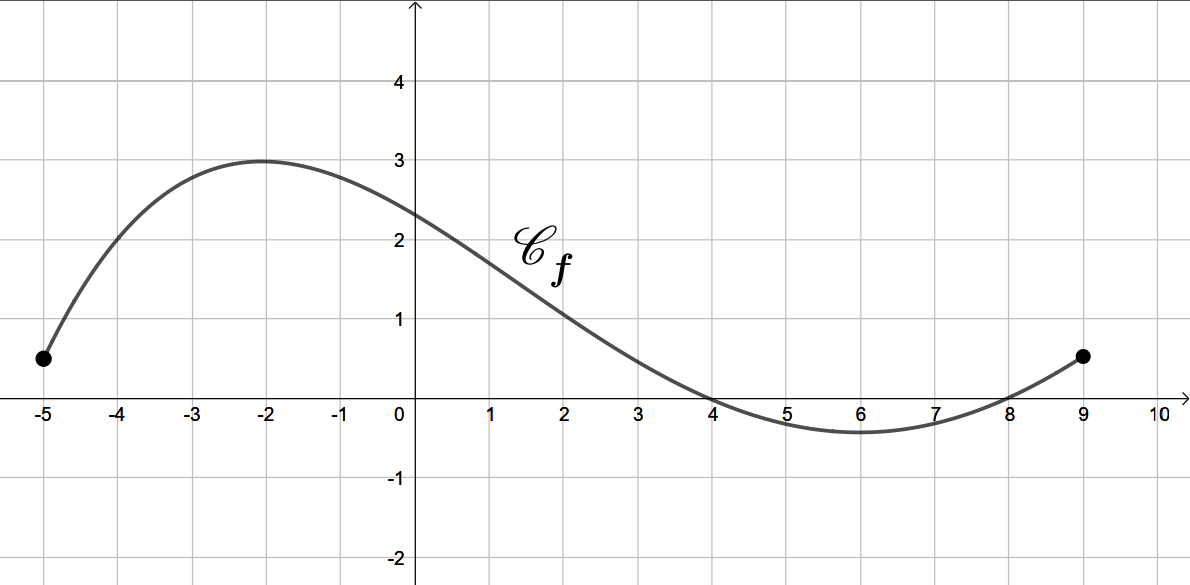 On admet également que , et que .
On admet également que , et que .

Question 1
Déterminer le domaine de définition de .
Correction
L'ensemble de définition de est .
Question 2
Déterminer l'image de .
Correction
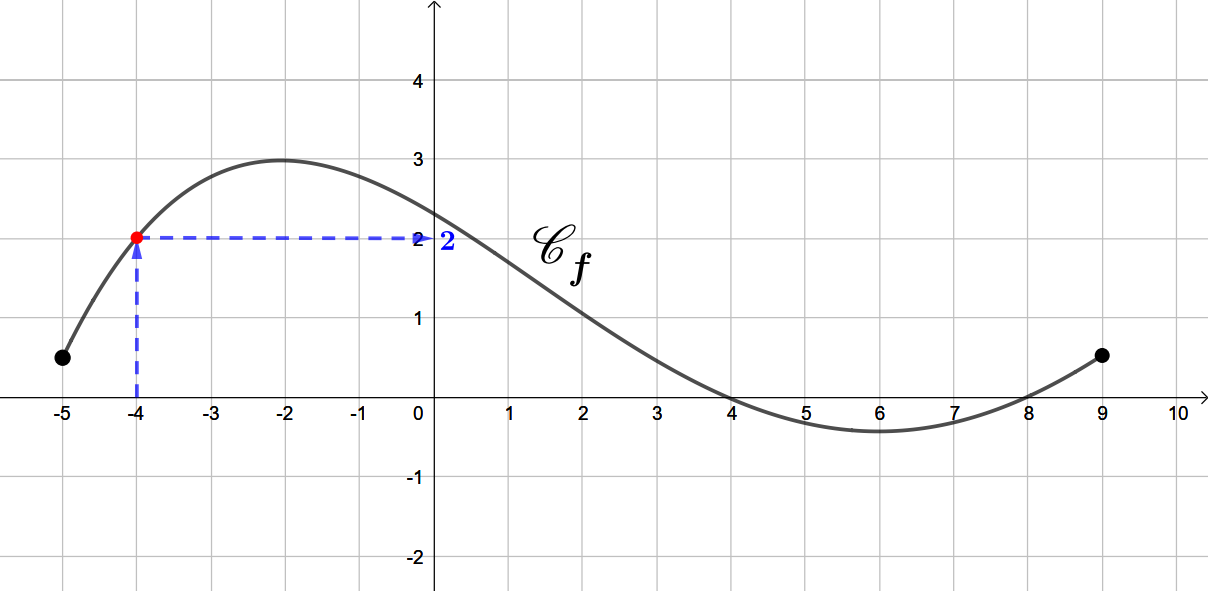
Pour cela :
On repère le point d'abscisse , et ensuite on rejoint la courbe verticalement.
Ensuite en partant du point de la courbe, on rejoint l'axe des ordonnées. (En ce point se trouve la valeur recherchée.)
A l'aide du graphique, on peut en conclure que l'image de par la fonction est . On peut l'écrire également :
Question 3
Déterminer le ou les antécédents de par .
Correction
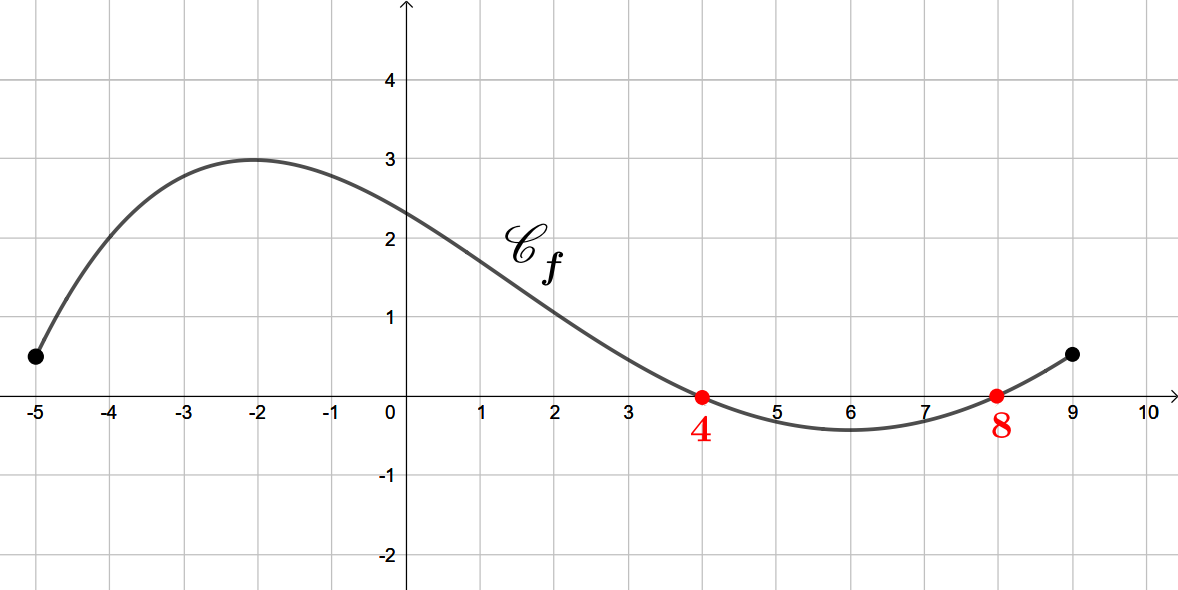
La courbe coupe l'axe des abscisses en deux points d'abscisses respectives et .
Par lecture graphique, les antécédents de par sont :
Question 4
Résoudre graphiquement l'équation
Correction
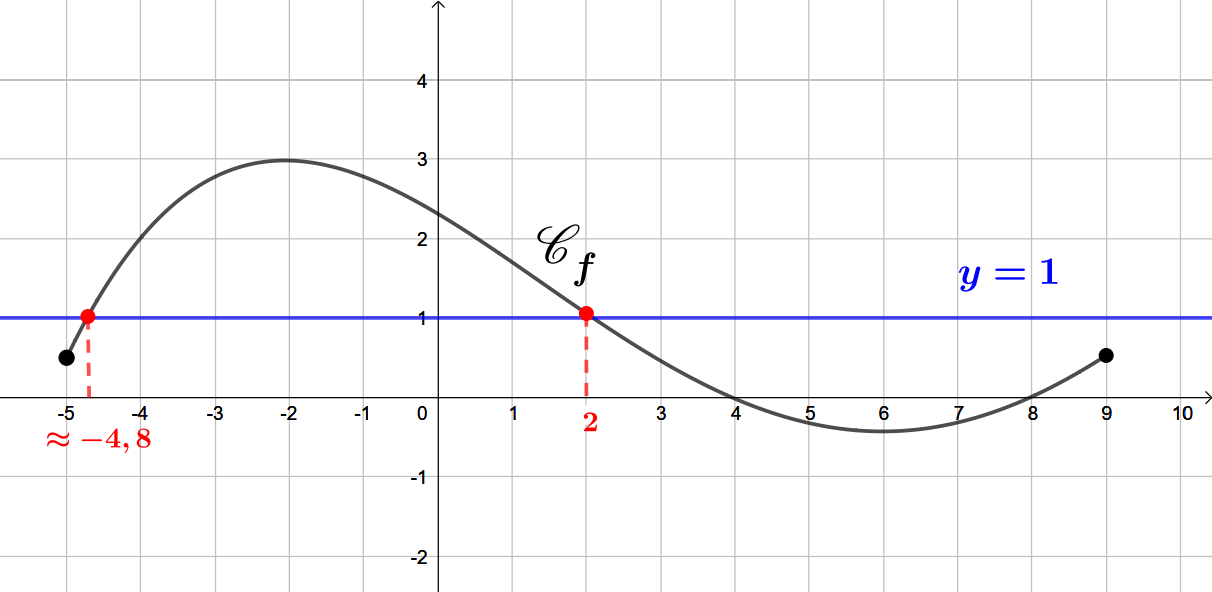
La droite d'équation coupe la courbe au point d'abscisse et .
Par lecture graphique, l'ensemble des solutions de l'équation est
Question 5
Donner une valeur de telle que n'admette aucune solution.
Correction

Il nous suffit de prendre une valeur de strictement plus grande que .
L'équation n'a donc pas de solution.
Question 6
Résoudre .
Correction
Question 7
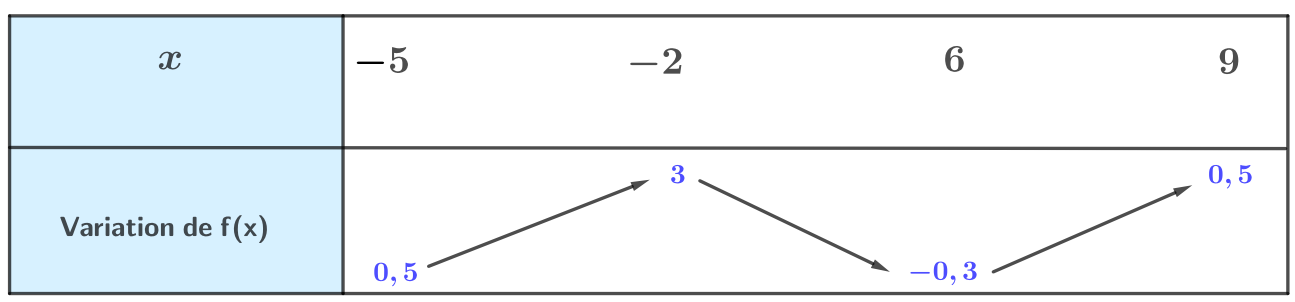
Dresser le tableau de variation de la fonction .
Correction

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.