Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Petits problèmes... - Exercice 3
25 min
45
Question 1
élèves d'un lycée font une dictée. On compte le nombre d'erreurs faits par élève. On présente les résultats à l'aide du tableau ci-dessous :


Calculer l'étendue de la série.
Correction
Question 2
Complétez le tableau avec les effectifs cumulés croissants. (ECC)
Correction

Question 3
Déterminer le premier quartile. Donner une interprétation du résultat.
Correction
Nous allons dans un premier temps reprendre le tableau avec la ligne des effectifs cumulés croissants. (ECC)
 Nous savons que .
Nous savons que . Pour déterminer le er quartile, on commence par calculer ce qui donne . Le er quartile, noté , correspond à la ème valeur de la série ordonnée (on arrondi toujours par excès si son écriture est décimal).
Ainsi :
(Dans la ligne des ECC on recherche la valeur si elle n'apparait pas on prend la valeur supérieur ici on prend et donc cela correspond à erreurs).

En italique ce sont des phrases explicatives qui ne doivent pas apparaitre sur vos copies, elles servent juste à vous expliquer le raisonnement.
Ainsi :
.
(Dans la ligne des ECC on recherche la valeur si elle n'apparait pas on prend la valeur supérieur ici on prend et donc cela correspond à erreurs).
Le premier quartile noté est la plus petite valeur de la série statistique telle qu’au moins des valeurs de la série sont inférieures ou égales à
Autrement dit , il y a au moins des élèves qui ont fait un nombre d'erreurs inférieur ou égal à .Question 4
Déterminer la médiane. Donner une interprétation du résultat.
Correction
Nous allons dans un premier temps reprendre le tableau avec la ligne des effectifs cumulés croissants. (ECC)
 Nous savons que .
Nous savons que .
Comme est pair, on agit de la sorte.
On indique que la médiane correspond à :
où ici
La ème valeur de la série est : .
La ème valeur de la série est : .
Ainsi :

En italique ce sont des phrases explicatives qui ne doivent pas apparaitre sur vos copies, elles servent juste à vous expliquer le raisonnement.
Pour déterminer la médiane, on commence par calculer ce qui donne .Comme est pair, on agit de la sorte.
On indique que la médiane correspond à :
où ici
La ème valeur de la série est : .
La ème valeur de la série est : .
Ainsi :
La médiane est la plus petite valeur de la série telle qu‘au moins des données soient inférieures à .
Autrement dit , il y a au moins des élèves qui ont fait un nombre d'erreurs inférieur ou égal à .Question 5
On donne le tableau ci-dessous avec la ligne des fréquences.


Remplir la ligne des fréquences dans le tableau ci-dessous. Il faudra donner des arrondis à près.
Correction
L’effectif d’une valeur du caractère étudié est le nombre d’individus de la population ayant cette valeur.
La fréquence d’une valeur est le quotient de l’effectif de cette valeur par l’effectif total de la population. (la fréquence peut être exprimée en pourcentage)
La formule est alors :
La fréquence d’une valeur est le quotient de l’effectif de cette valeur par l’effectif total de la population. (la fréquence peut être exprimée en pourcentage)
La formule est alors :
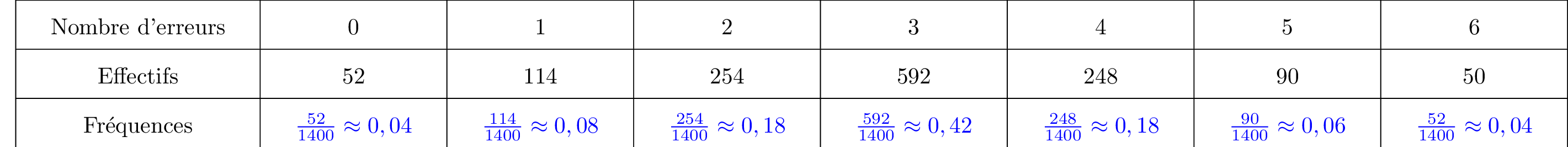
Question 6
Donner la fréquence des élèves qui ont eu erreurs dans la dictée.
Correction
D'après la question , nous savons que : 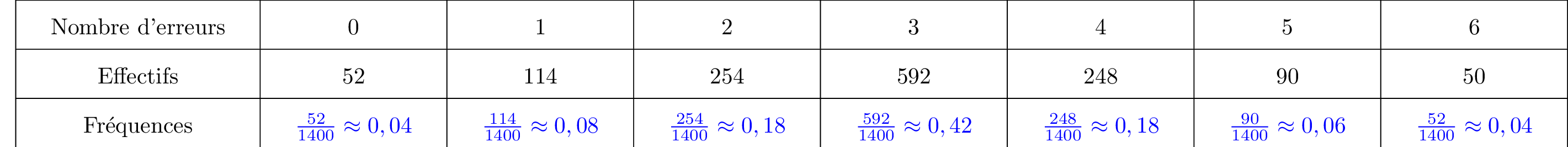 La fréquence des élèves qui ont eu erreurs dans la dictée est de qui correspond à des élèves.
La fréquence des élèves qui ont eu erreurs dans la dictée est de qui correspond à des élèves.
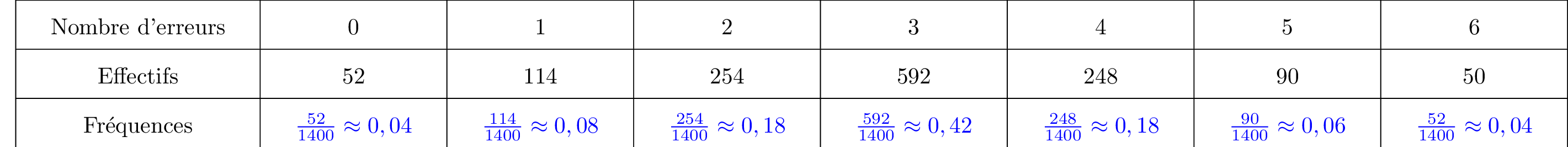
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.