Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Petits problèmes... - Exercice 2
25 min
45
Question 1
Le lycée Molière présente ci-dessous, la répartition des âges de tous ses élèves.


Complétez le tableau avec les effectifs cumulés croissants. (ECC)
Correction

Question 2
Calculer l'âge moyen des élèves de ce lycée.
Correction

La moyenne d'une série statistique est le réel, noté , tel que :
Ici, correspond à l'effectif total, c'est à dire : . Il vient alors que :
.
L'âge moyen des lycées est de ans après arrondi à près.
Question 3
Déterminer le premier quartile. Donner une interprétation du résultat.
Correction

En italique ce sont des phrases explicatives qui ne doivent pas apparaitre sur vos copies, elles servent juste à vous expliquer le raisonnement.
Ainsi :
.
(Dans la ligne des ECC on recherche la valeur si elle n'apparait pas on prend la valeur supérieur ici on prend et donc cela correspond à ans)
Le premier quartile noté est la plus petite valeur de la série statistique telle qu’au moins des valeurs de la série sont inférieures ou égales à
Autrement dit , il y a au moins des élèves qui ont un âge inférieur ou égal à ans.Question 4
Déterminer le troisième quartile. Donner une interprétation du résultat.
Correction

En italique ce sont des phrases explicatives qui ne doivent pas apparaitre sur vos copies, elles servent juste à vous expliquer le raisonnement.
Ainsi :
.
(Dans la ligne des ECC on recherche la valeur si elle n'apparait pas on prend la valeur supérieur ici on prend et donc cela correspond à ans)
Le troisième quartile noté est la plus petite valeur de la série statistique telle qu’au moins des valeurs de la série sont inférieures ou égales à
Autrement dit , il y a au moins des élèves qui ont un âge inférieur ou égal à ans.Question 5
Déterminer la médiane. Donner une interprétation du résultat.
Correction

En italique ce sont des phrases explicatives qui ne doivent pas apparaitre sur vos copies, elles servent juste à vous expliquer le raisonnement.
Pour déterminer la médiane, on commence par calculer ce qui donne .La médiane, notée , correspond à la ème valeur de la série ordonnée (ici, nous avons un effectif total impair et dans ce cas on arrondi toujours par excès si son écriture est décimal).
Ainsi :
.
(Dans la ligne des ECC on recherche la valeur si elle n'apparait pas on prend la valeur supérieur ici on prend et donc cela correspond à ans).
La médiane est la plus petite valeur de la série telle qu‘au moins des données soient inférieures à .
Autrement dit , il y a au moins des élèves qui ont un âge inférieur ou égal à ans.Question 6
Représenter la boite à moustache de cette série.
Correction
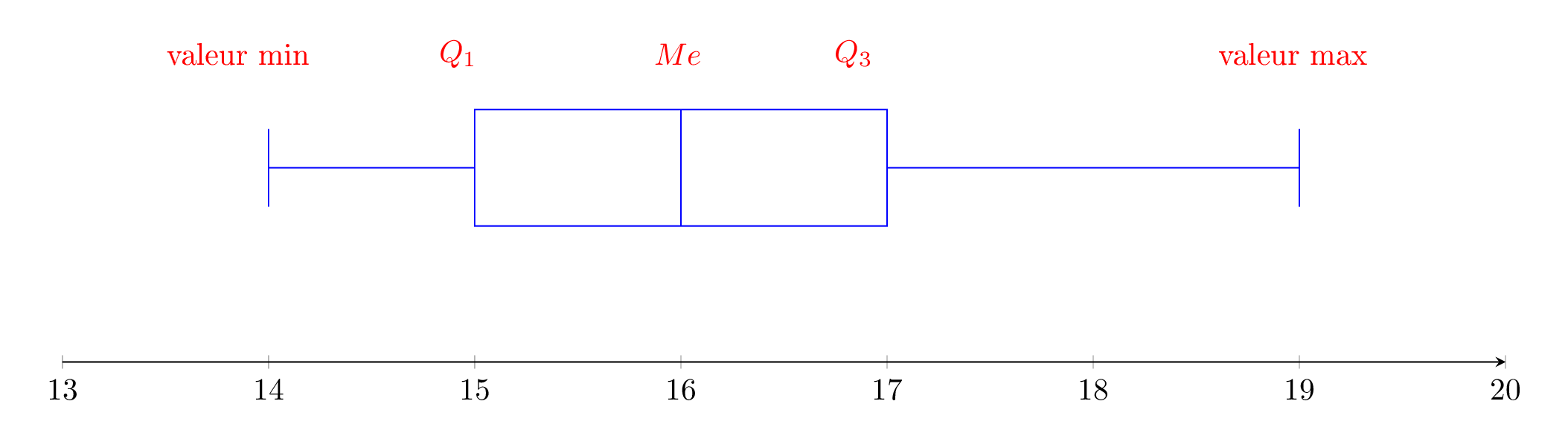
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.