Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Exercices types : 22ème partie - Exercice 2

20 min
40
Question 1
Avant de rendre les copies à ses élèves, un professeur de mathématiques présente à ses 2626 élèves de 22A leurs résultats à l'aide d'une boite à moustache donnée ci-dessous :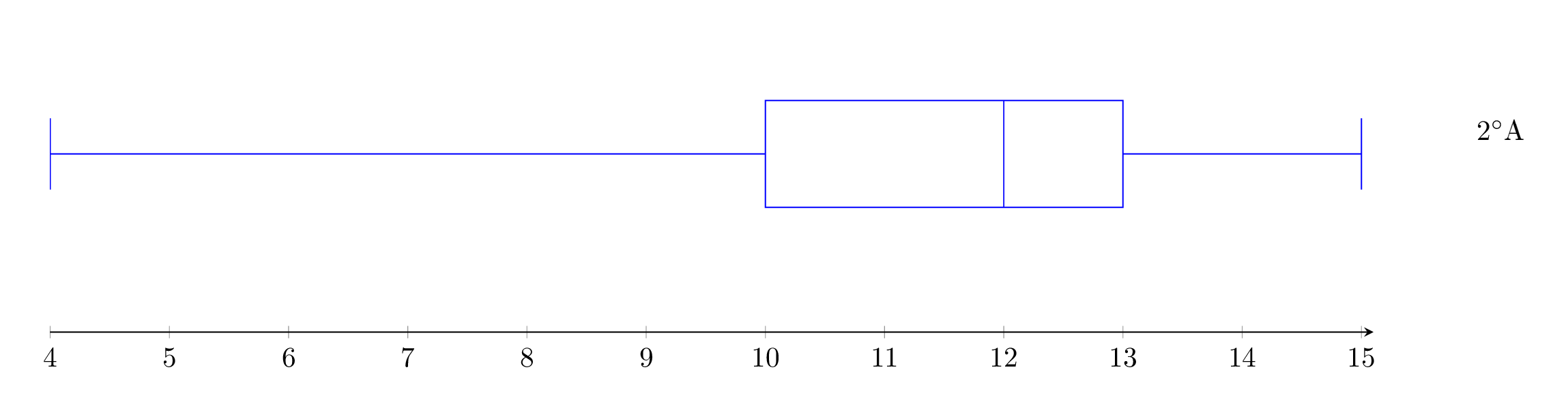
Il indique en outre que la moyenne de la classe est de 11,5/2011,5/20 .

A partir du diagramme en boite, donner la valeur des paramètres suivants : 11er quartile; 33ème quartile; la médiane, l'étendue; l'écart interquartile; la note minimale et la note maximale.

Correction
Nous avons compléter sur la boire à moustache les informations demandées. Nous pouvons lire que :
  • 11er quartile : Q1=10Q_{1}=10
  • 33ème quartile : Q3=13Q_{3}=13
  • Médiane : Me=12Me=12
  • Ecart interquartile : Q3−Q1=13−10=3Q_{3}-Q_{1}=13-10=3
  • Note minimale : 44
  • Note maximale : 1515
  • L’étendue est la différence entre la plus grande et la plus petite valeur d’une série statistique.
    • eˊtendue=15−4\text{étendue}=15-4
    eˊtendue=11\text{étendue}=11

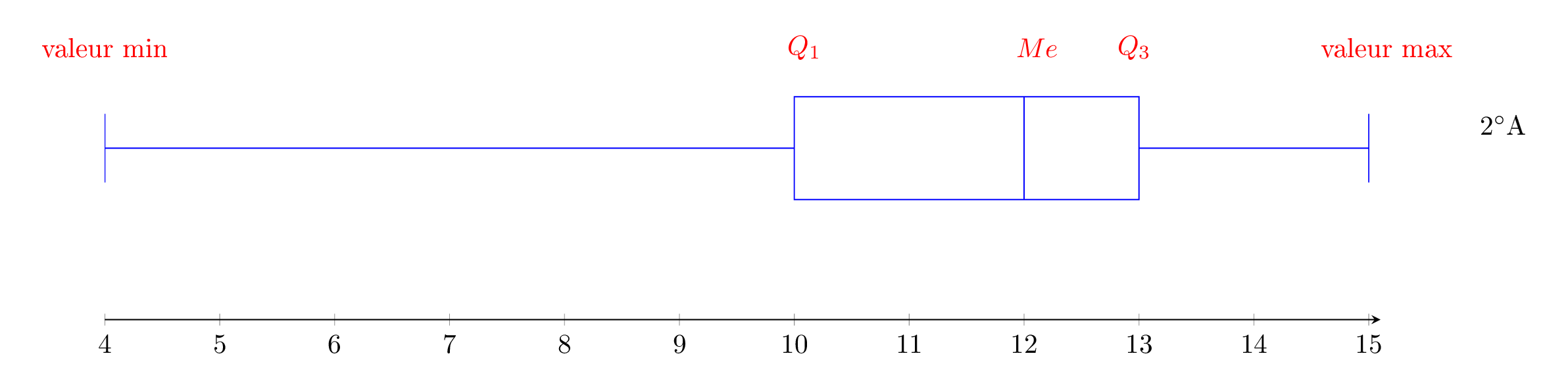
    Question 2
    Répondre par vrai ou faux aux affirmations suivantes :

    La moitié des élèves ont une note en dessous de 11,511,5.

    Correction
    La proposition est FAUSSE.
    La médiane est la plus petite valeur de la série telle qu‘au moins 50%50\% des données soient inférieures à MeMe.
    La médiane est de 1212 donc la moitié des élèves ont une note en dessous de 1212.
    Question 3

    La moitié des notes de la classe se situent entre 1010 et 1313.

    Correction
    La proposition est VRAIE.
    L'écart interquartile d'une série mesure la dispersion autour de la médiane. Il contient au moins 50%50\% des valeurs de la série.
    Nous savons que Q1=10Q_{1}=10 et Q3=13Q_{3}=13 . La moitié des valeurs d’une série sont comprises entre Q1Q_{1} et Q3Q_{3} .
    Question 4

    La médiane est la 1313ème note dans la série des notes rangées dans l’ordre croissant.

    Correction
    La proposition est FAUSSE.
    Nous savons que l'effectif de la classe est N=26N=26. Ici, NN est pair.
    Commençons par calculer N2=262=13\frac{N}{2}=\frac{26}{2}=13.
    Comme NN est pair, on agit de la sorte.
    On indique que la médiane MeMe correspond à :
    Me=(N2)eˋme valeur de la seˊrie+(N2+1)eˋme valeur de la seˊrie2Me=\frac{\left(\frac{N}{2}\right)\text{ème valeur de la série} + \left(\frac{N}{2}+1\right)\text{ème valeur de la série}}{2} où ici N2=13\frac{N}{2}=13
    Me=13 eˋme valeur de la seˊrie+14 eˋme valeur de la seˊrie2Me=\frac{\text{13 ème valeur de la série} + \text{14 ème valeur de la série}}{2}
    Question 5

    Il y a au moins un élève qui a eu 1010.

    Correction
    La proposition est VRAIE.
    Q1=10Q_{1}=10 . Les quartiles appartiennent nécessairement à la série.

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.