Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Tchat avec un prof
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Déterminer la médiane, le 1er quartile et le 3ème quartile - Exercice 2
16 min
30
Après avoir postulé et été acceptée sur un poste de directrice des ressources humaines, Lina souhaite connaitre la politique salariale de sa nouvelle entreprise.
Elle établit le tableau suivant :
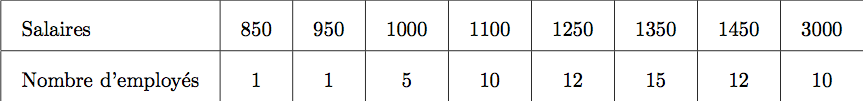
Elle établit le tableau suivant :
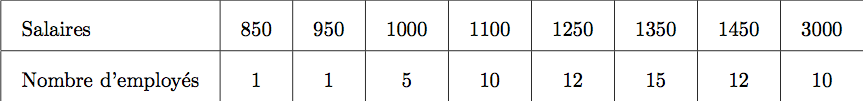
Question 1
Calculer le er quartile.
Correction
En italique ce sont des phrases explicatives qui ne doivent pas apparaître sur vos copies, elles servent juste à vous expliquer le raisonnement.
On va commencer par définir les effectifs cumulés croissants (ECC}.

On note
Pour déterminer le er quartile, on commence par calculer ce qui donne .
Le 1er quartile, noté , correspond à la ème valeur de la série ordonnée (on arrondi toujours par excès si son écriture est décimal).
Ainsi :
.
(Dans la ligne des ECC on recherche la valeur ici apparaît et donc cela correspond à ).
Question 2
Calculer le ème quartile.
Correction
On reprend le tableau des effectifs cumulés croissants.

Pour déterminer le ème quartile, on commence par calculer ce qui donne .
Le ème quartile, noté , correspond à la ème valeur de la série ordonnée (on arrondi toujours par excès si son écriture est décimal).
Ainsi :
(Dans la ligne des ECC on recherche la valeur si elle n'apparait pas on prend la valeur supérieur ici on prend et donc cela correspond à ).

Pour déterminer le ème quartile, on commence par calculer ce qui donne .
Le ème quartile, noté , correspond à la ème valeur de la série ordonnée (on arrondi toujours par excès si son écriture est décimal).
Ainsi :
.
(Dans la ligne des ECC on recherche la valeur si elle n'apparait pas on prend la valeur supérieur ici on prend et donc cela correspond à ).
Question 3
Calculer la médiane.
Correction
On reprend le tableau des effectifs cumulés croissants.

Pour déterminer la médiane, on commence par calculer ce qui donne .
Ici, est pair, donc on n'écrira pas que la médiane, otée , correspond à la ème valeur de la série ordonnée.
Dans le cas où est pair, on agit de la sorte.
On calcule .
Puis on indique que la médiane correspond à :
où ici
La ème valeur de la série est : .
La ème valeur de la série est : .
Ainsi :

Pour déterminer la médiane, on commence par calculer ce qui donne .
Ici, est pair, donc on n'écrira pas que la médiane, otée , correspond à la ème valeur de la série ordonnée.
Dans le cas où est pair, on agit de la sorte.
On calcule .
Puis on indique que la médiane correspond à :
où ici
La ème valeur de la série est : .
La ème valeur de la série est : .
Ainsi :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.